Considera la ecuación diferencial 5y^''+y^'=-6x.
ayuda para este problema de ecuaciones diferenciales
Considera la ecuación diferencial 5y^''+y^'=-6x.
- Encuentra la solución general de la ecuación diferencial
- Encuentra la solución sujeta a las condiciones iniciales:
.y(0)=0, y^' (0)=-10
- Gráfica la solución la solución encontrada en b).
Respuesta de Lucas m
1
Enrique Gonzales!
Es una ecuación diferencial lineal con coeficientes constantes y no homogénea:
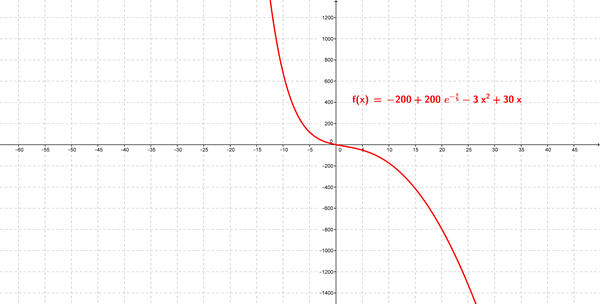
$$\begin{align}&Ec. Homogénea\\ &5y''+y'=0\\ &\\ &Ec.Característica\\ &5D^2+D=0\\ &D_1=0\\ &D_2=\frac{-1}{5}\\ &Soluciòn \ de \ la \ homogénea\\ &y_h=C_1e^0+C_2e^{-x/5}\\ &\\ &y_h=C_1+C_2e^{-x/5}\\ &\\ &La \ solución \ particular \ será \ del \ tipo \\\ &y_p=Ax^2+Bx\\ & En \ primer \ lugar \ escogemos \ un \ polinomio \ de \ grado \ 2 \ para \ que\\ &el \ primer \ miembro \ de \ la \ ED \ sea \ un \ polinomio \ de \ grado \ 1. Y \ lo \ \\ &escogemos \ \sin \ término \ independiente \ porque \ al \ sustituirlo \ en\\ &la \ ED\ nos \ da \ cero.\\ &y_p=Ax^2+Bx\\ &y'=2Ax+B\\ &y''=2A\\ &Sustituyendo \ en \ ED\\ &5(2A)+(2Ax+B)=-6x\\ &2Ax+(10A+B)=-6x\\ &\Rightarrow2A=-6 \Rightarrow A=-3\\ &\Rightarrow10A+B=0 \Rightarrow B=30\\ &y_p=-3x^2+30x\\ &\\ &y_G=y_h+y_p\\ &\\ &y_G=C_1+C_2e^{-x/5}-3x^2+30x\\ &\\ &b) y'=\frac{-1}{5}C_2e^{-x/5}-6x+30\\ &\\ &y(0)=0 \Rightarrow C_1+C_2=0\\ &y'(0)=-10\Rightarrow-\frac{1}{5}C_2+30=-10\Rightarrow C_2=200 \Rightarrow C_1=-200\\ &\\ &Sol.\\ & y=-200+200e^{-x/5}-3x^2+30x\\ &\\ &\end{align}$$Gráfica:
Un placer
Como nuevo en el chat has de saber que lo único que se pide es valorar la respuesta.
Excelente es lo correcto
