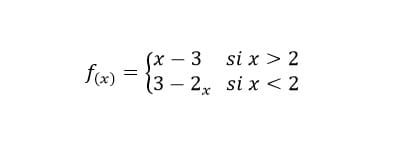¿Puedes calcular los limites cuando”X” tiende a 2?

·

Has escrito un 2 con subíndice x en la segunda definición de la función, eso no tiene ningún significado, seguramente querías decir el producto 2x.

Los límites son dos, por la izquierda y la derecha. Cuando ambos existen y son iguales decimos que existe el límite en ese punto.

Para el límite por la izquierda tomaremos la definición

3-2x   si x < 2

Ya que los puntos de la izquierda de 2 son los menores que 2

Entonces

$$\begin{align}&\lim_{x\to 2^-} f(x) = \lim_{x \to 2^-}(3-2x) = 3-2·2 = 3-4=-1\end{align}$$

Y por la derecha tomaremos la parte de la función que se refiere a los puntos mayores que 2

$$\begin{align}&\lim_{x\to 2^+} f(x) = \lim_{x \to 2^+}(x-3) =2-3=-1\end{align}$$

Y ambos límites coinciden, luego podemos decir que

$$\begin{align}&\lim_{x\to 2}f(x) = -1\end{align}$$

--------

Para que una función sea continua en un punto debe tener un valor que coincida con el límite de la función en ese punto. Y en este caso la función no tiene un valor ya que nos dicen lo que vale cuando es menor o mayor que 2, pero para el valor x=2 no nos dan el valor de la función. Y al no tener valor, la función no es continua en x=2

Si uno de los dos signos de la desigualdad hubiera sido menor o igual, o mayor o igual, sí habría sido continua ya que su valor habría sido .1 que coincidía con el límite, pero tal como está no es continua.