Ejercicio de Ecuaciones diferenciales: Representación de un modelo matemático
Me podrían auxiliar en la resolución del siguiente ejercicio.
En una cierta población la rapidez de nacimientos y de muertes es proporcional a la cantidad de individuos vivos en un momento dado. El siguiente esquema da una mejor idea del fenómeno. Y es el número de individuos presentes en la población en cualquier instante t.
Nacimientos (Y) muertes
Encontrar el modelo matemático del comportamiento del crecimiento de esta población, el cual debe incluir lo siguiente.
- a) Rapidez de nacimientos.
- b) Rapidez de muertes.
- c) Rapidez de cambio del número de individuos en la población.
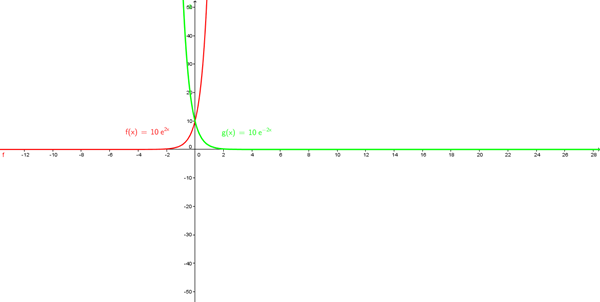
Resuelve las ecuaciones diferenciales que resultan en cada inciso. En el inciso c puedes dar valores arbitrarios a las constantes que resulten, para poder graficar.
1 Respuesta
1)Rapidez de Nacimientos es proporcional al numero de individuos en ese instante N
$$\begin{align}&\frac{dN}{dt}=kN\end{align}$$2) Rapidez de Muertes también es proporcional a N
$$\begin{align}&\frac{dN}{dt}=qN\end{align}$$3) Variación de la Población
$$\begin{align}&\frac{dN}{dt}=kN-qN\\&\\&\frac{dN}{dt}=N(k-q)\\&\\&k-q=r \Rightarrow\\&\\&\frac{dN}{dt}=Nr\\&\\&ED \ Variables \ Separables:\\&\\&\frac{dN}{N}=r·dt\\&\\&\int \frac{dN}{N}=\int r·dt\\&\\&lnN=rt+C_1\\&\\&N=e^{rt+C_1}\\&N=e^{rt}·e^{C_1}\\&C=e^{C_1}\\&\\&N=Ce^{rt}\\&\end{align}$$Espero que te sirva.
Saludos
Hola Apreciable Lucas
Muy bien el planteamiento, una duda más, si le añadiera valores numéricos cualesquiera, como quedarían las ecuaciones, muchas gracias por tu apoyo.
Pues com esta en las gráficas
He puesto C=10
Y dos casos
r>0 la población crece
r<0 la población decrece
Faltaria r=0, don de la función queda y=C constante
