Pueden ilustrar como realizar el siguiente ejercicio de derivada
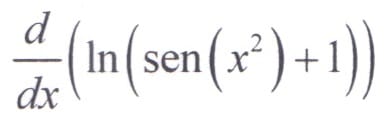
Estoy estancado en este ejercicio si alguien me puede ayudar se lo agradecería
2 Respuestas
Respuesta
1
Respuesta de Valero Angel Serrano Mercadal
1
