Resuelve los siguientes planteamientos que se presentan a continuación:gráfica la curva f(x)=x^3-4x

·

Depende del nivel de estudios que lleves. Supongo que ya has dado límites, derivadas, máximos, mínimos, crecimiento, concavidad, etc.

Bueno, el dominio es (-∞,∞)

Tiene simetria respecto del punto origen ya que

f(x) =-f(-x)

f(x)= x^3 - 4x = -(-x)^3 + 4(-x) = -[(-x)^3 - 4(-x)] =-f(-x)

No tiene ninguna clase de asíntota ni periodicidad.

Es continua.

Los cortes con el eje X son

x^3 - 4x=0

x1=0

x^2-4 = 0

x^2 = 4

x2=-2

x3=2

Y el corte con el eje Y es (0,0)

·

Derivamos e igualamos a 0 para ver los puntos críticos

f '(x) =3x^2-4=0

3x^2 = 4

x^2 = 4/3

x = +- 2/sqrt(3)

donde sqrt significa raíz cuadrada

La derivada segunda es

f''(x) =6x

Cuando tomamos -2/sqrt(3) la derivada segunda es negativa luego es un máximo

El máximo aproximado es x=-1.1547

Y el valor de la función es f(-1.1547) = 3.0792

El punto del máximo es (-1.1547, 3.0792)

Cuando tomamos 2/sqrt(3) la derivada segunda es negativa luego es un mínimo.

Y por la simetría central que decíamos el mínimo es el punto

(1.1547, -3.0792)

Es creciente al principio cuando parte de -∞ hasta llegar al máximo, luego decrece hasta llegar al mínimo y finalmente crece hasta el infinito.

( -∞, -1.1547) creciente

(-1.1547, 1.1547) decreciente

(1.1547, ∞) creciente

La derivada segunda se anula para x=0 y antes de x=0 es negativa luego es cóncava hacia abajo, forma de iglú, y a partir de x=0 es positiva, luego es cóncava hacia arriba, tienen forma de U.

( -∞.0) Cóncava hacia abajo

(0, ∞) cóncava hacia arriba

·

Yo creo que estos son los datos necesarios para boquejar la gráfica. Si se quiere hacer mejor se hace una tabla de puntos.

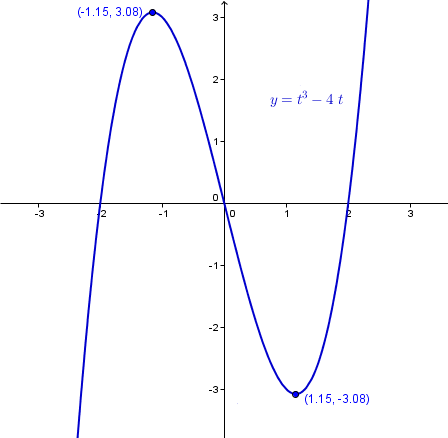
Y eso es todo.