Anónimo
Movimiento circular de un cuerpo
Mi hermano me pidio ayuda para este ejercicio y no le entendí, podría ayudarme
Movimiento circular de un cuerpo.
Un satélite artificial a una altura de 400 kilómetros sobre la superficie da una vuelta a la Tierra en 93 minutos. Considera el radio terrestre de 6400 km.
- Escribe la posición del satélite en términos del tiempo, x(t), y(t). Considera lo siguiente:
- Marca un punto en el satélite. La descripción del movimiento será la relativa a este punto y con respecto al centro de la Tierra.
- Usa tu escala adecuadamente para obtener los valores de las posiciones en metros.
- En una tabla, anota los valores de las posiciones en x y y, para una vuelta completa del satélite
- Una gráfica de los valores de las posiciones y vs. x te dará la trayectoria del satélite.
- Una gráfica de las posiciones del tren en x y y contra el tiempo será sinusoidal, con amplitud igual al radio de la trayectoria. Obtén el periodo del movimiento del satélite de estas gráficas.
- Calcula las velocidades en x y y. Al graficar, obtendrás un comportamiento sinusoidal, con amplitudes iguales a la velocidad lineal del satélite. Se puede comprobar esta velocidad lineal con la circunferencia de la trayectoria entre el periodo de una revolución.
- Calcula y grafica los valores para la aceleración lineal. Las gráficas aceleración vs. Tiempo deberían tener amplitudes iguales a la aceleración centrípeta del satélite.
- Aplica el teorema de Pitágoras a los valores de las posiciones en x y y para obtener el radio de la trayectoria.
- Usa la función tangente inversa para obtener datos del movimiento rotacional, ϴ(t).
- Grafica el ángulo contra el tiempo, ϴ(t), y de la pendiente obtén la velocidad rotacional del satélite.
- Presenta tus resultados en tablas de Excel.
- Presenta tus gráficas utilizando un software de graficación
Te anticipo algunos de los cálculos que necesitarás para encarar tu desarrollo…..
La trayectoria del satelite la puedes representar como funcion de x = distancia en horizontal e y= distancia en vertical. El satélite se mueve en un plano constante y consideramos nuestro sistema con origen en el centro de la Tierra. ( Según dice el enunciado).
Suponiendo la órbita circular con un periodo de 93 = 5580 segundos imaginaríamos que el satélite se mueve en un plano fijo que pasa por el centro de la Tierra y que contiene al eje de rotación terrestre.
El radio de la orbita seria = 6400 + 400 = 6800 Km = 6.80 x (10)6 metros. Si consideramos como origen el centro de la tierra los valores de x e y variarán sinusoidalmente sobre cada eje de coordenadas. Es decir serán funciones armónicas del tiempo…con los valores característicos:
Amplitud = Radio de la trayectoria = 6.8 x (10)6 metros.
La velocidad tangencial = Radio orbital x 2pi / periodo = 6.8 x (10)6 x 6.28 / 93x60 seg. = 7653 m/seg.
La aceleración ( centrípeta) = (7653 m/seg) 2 / 6.8 x (10)6 m = 8.61 m/seg2
El movimiento proyectado sobre los ejes coordenados serán sendas sinusoides de pulsación w = 6.28/93 x 60 = 0.001125 / seg……y frecuencia = 1/T = 1/ 93x60 = 0.000179 Hz. Estas sinusoides estarán defasadas en pi/2 radianes entre si.
x(t) = = 6.8 x (10)6 sen 0.001125 t……………………..y(t) = = 6.8 x (10)6 cos 0.001125 t
La composición de x(t) e y(t) te dará la circunferencia que representa el radio de la trayectoria. La coordenadas polares las obtienes de x=Ro sen fi ….y = Ro cos fi con Ro = = 6.8 x (10)6
El tabulado en Excel y el Software te lo dejo para que investigues y lo armes vos.
Buen día me quedo con dudas en el punto -En una tabla, anota los valores de las posiciones en x y y, para una vuelta completa del satélite, en base a que, si es un satélite y gira alrededor de la tierra solo va a dibujar un circulo, ahora en el punto - Una gráfica de los valores de las posiciones y vs. x te dará la trayectoria del satélite. Como se supone que haré la gráfica está muy confuso
Trata de armar un cuadro como el que te dibujo y de allí podrás obtener todo lo que te están pidiendo. Utilizas las fórmulas que te di en respuesta anterior. Puedes partir de x=0 e y= 6.8 x 10^6 metros girando en sentido contrario al reloj.
Perdón... yo lo estoy calculando girando en el sentido horario...
At. Brenda
Bueno………. Por un lado supone que vas a evaluar la posición x, y del satélite partiendo desde la vertical a tu cuerpo. O sea desde la posición zenital. Comienzas a describir el MCU tomando como posición inicial x=0 …y = 6.80 x (10)6 metros…. La vertical sobre tu cabeza……
Para tener puntos sucesivos de la trayectoria divides la órbita – circunferencia – en 20 partes .Y vamos a tomar el sentido de marcha como el del reloj………
Según te explique antes, si el periodo ( 2pi rad.) dura 93 minutos= 5580 segundos. Cada una de las 20 avas partes representara un tiempo de 5580/20=279 seg. Que corresponde al valor angular 2pi/20 = 0.314 rad.
Tambien te había dicho antes que las ecuaciones de la trayectoria en x e y significaban sendas sinusoides .x(t) = 6.80 x 106 sen wt…………….y(t)= 6.80 X 106 cos wt…..con w = 2pi/T = 6.28 / 5580 = 0.001125 / seg.
Luego….si el primer punto lo tomo sobre mi cabeza ( cenit) serían x=0……..y= 6.80 x (10)6…a los que correspondería el angulo φ = 90° = pi/2 rad. = 1.57 rad………De aquí hallas el modulo =y= 6.80 x (10)6 m.
Para el segundo punto .t= 279 seg. Después.. el satélite se hallara en un punto del espacio tal que:
X= 6.80 x 106 sen( 0.001125 x 279) = 6.80 x 106 sen 0.3138 = 6.80 x (10) 6 x 0.308 = 2 x 106 m.
Y= 6.80 x 106 cos( 0.001125 x 279) = 6.80 x 106 cos 0.3138 = 6.80 x (10)6 x 0.951 = 6.468 x 106 m
Modulo = Ro = V (2X2) + (6.468 X 6.468) = 6.78 X (10)6 metros.
Angulo de visión = angulo φ = +90 – 18 = 72° ….en radianes = 1.256 rad.
Para el tercer punto de la trayectoria t= 2 x 279 = 558 seg….el satélite se hallara en:
X= 6.80 x 106 sen ( 0.001125 x 558) = 6.80 x 106 x 0.587 = 4 x (10)6 m.
Y= 6.80 x 106 cos ( 0.001125 x 558) = 6.80 x 106 x 0.809 = 5.50 x (10)6 m.
Modulo = Ro = igual que antes resulta 6.80 x (10)6 metros.
Angulo= angulo φ= +90 – (2x18) = 54° …en radianes = 0.942 rad.
Y así sucesivamente …. Vas completando el cuadro.
Ojo! Los argumentos siempre significan radianes ( no grados ).
Las coordenadas polares las obtienes de x=Ro cos φ ….y = Ro sen φ ………con Ro = = 6.8 x (10)6
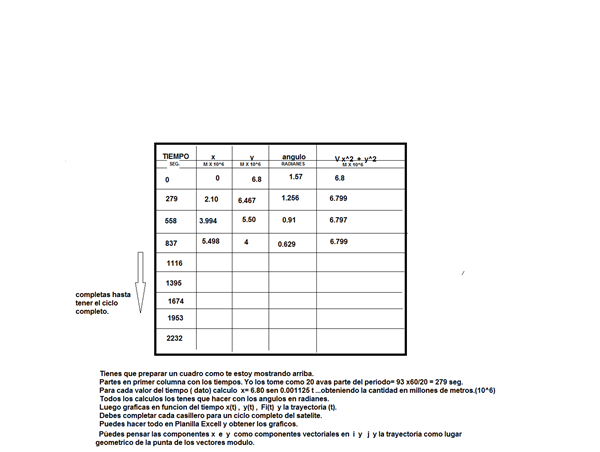
Analizando la tabla y su respuesta no logro descifrar como esta sacando los valores de X, Y y los radianes - Brenda Reyes