Hallar Ecuación vértice y pendiente parábola
Amigos he intentado e intentado y no he podido con este ejercicio no se si esté mal formulado
Gracias
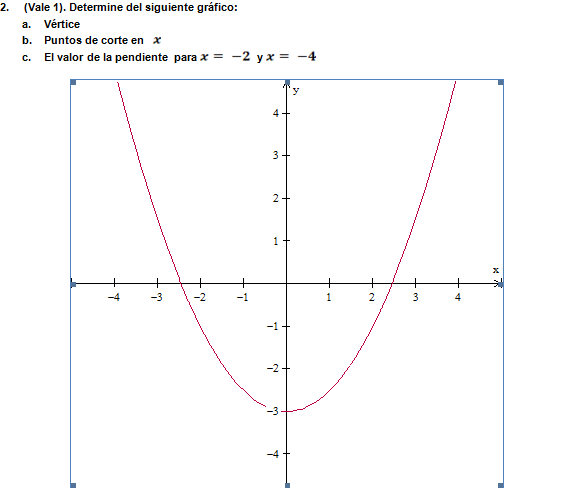
2 respuestas
Henry Bentiez!
La parábola dibujada es del tipo
$$\begin{align}&y=ax^2-3\end{align}$$por tener el vértice en el eje de ordenadas (b=0)
Para calcular el valor exacto de a, necesitamos la coordenada de otro punto de la parábola. Mira si pasa por algún otro punto determinado, con el dibujo de arriba es imposible saber.
Es decir que la profesora formuló mal el punto?
Necesitamos otro punto exacto de la parábola, para poder determinar elcoeficiente principal.
Tendrías que votar la respuesta.
Excelente es lo correcto.
Tendrías que votar Excelente a todos los expertos que te contesten una pregunta de
Matemáticas.
·
Solo sabemos que el vértice es el punto (0, -3)
Una parabola tiene por ecuación
f(x) = ax^2 + bx + c
Y el vértice tiene coordenada x=-b/2a
Como la coordenada x del vértice es 0 sera
-b/2a = 0
-b = 0
b=0
Luego de momento queda reducida a
f(x) = ax^2 + c
Por pasar por (0,-3) se cumple
-3 = a·0^2 + c
c=-3
Con l cual la función es
f(x) = ax^2 - 3
Y del dibujo aun se puede deducir que a>0 por ser creciente cuando x>0
Pero no se puede deducir más se necesitaría conocer otro punto exacto de la parábolo para poder calcular a.
Tal como lo tenemos se puede calcular pero de forma genérica.
Los puntos de corte con el eje X serán
$$\begin{align}&0 = ax^2 - 3\\&\\&ax^2 = 3\\&\\&x^2 = \frac 3a\\&\\&x=\pm \sqrt \frac 3a\\&\\&\text{La pendiente es la derivada}\\&\\&f'(x) = 2ax\\&\\&f'(-2) = 2a(-2) = -4a\\&\\&f'(-4)=2a(-4) = -8a\end{align}$$Y eso es todo.