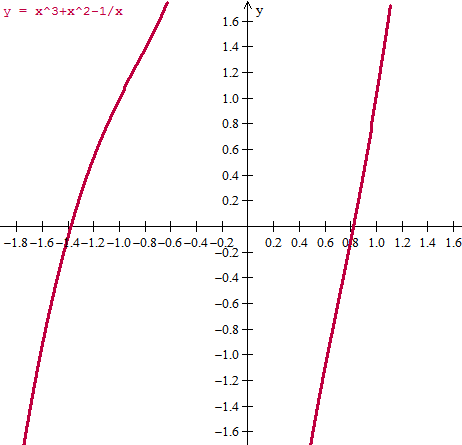Hallar el punto donde se interceptan las dos curvas: f(x)=x^3 + x^2 y f(x)=1/x :

·

El método de Newton sirve para solucionar ecuaciones del tipo

f(x)=0

Si tú tienes que encontrar los puntos de intersección de f(x) y g(x) las tienes que igualar

f(x) = g(x)

Y luego pasas g(x) al lado izquierdo

f(x)-g(x) = 0

si llamas h(x)=f(x)-g(x) ya tienes una ecuación

h(x)=0

que se puede resolver con el método de Newton.

·

Yo no sé cómo de evolucionada será la teoría que habéis dado del método de Newton. El método de Newton presenta problemas muchas veces si no se le da un valor inicial bastante próximo a la respuesta, luego es un método que hay que controlarlo muy bien. Por eso no me gusta mucho, pero vamos con él

x^3 + x^2 = 1/x

x^3 + x^2 - 1/x = 0

Y por lo que te decía de que se necesita una buena aproximación inicial lo mejor será hacer la gráfica

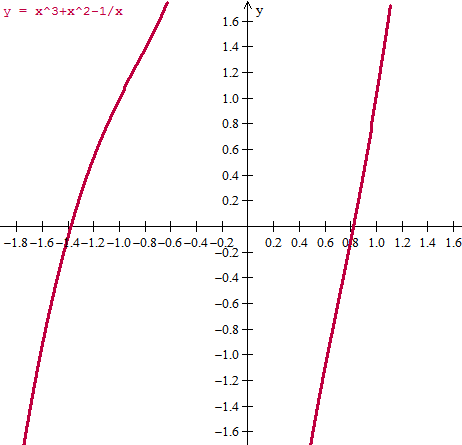
Luego tomaremos como valores iniciales

-1.4

0.8

Y la sucesión del método de Newton es

$$\begin{align}&x_n=x_{n-1}-\frac{f(x_{n-1})}{f'(x_{n-1})}\\&\\&x_n=x_{n-1}-\frac{x_{n-1}^3+x_{n-1}^2-\frac{1}{x_{n-1}}}{3x_{n-1}^2+2x_{n-1}+\frac{1}{x_{n-1}^2}}\\&\\&\text{Y ahora vienen muchas cuentas, una}\\&\text{buena calculadora u odenador mejor}\\&\\&x_0= -1.4\\&\\&x_1=(-1.4)-\frac{(-1.4)^3+(-1.4)^2-\frac{1}{(-1.4)}}{3(-1.4)^2+2(-1.4)+\frac{1}{(-1.4)^2}}=\\&-1.380582082764893\\&\\&x_2=\text{Todo eso con -1.380582082764893}=\\&-1.380277642644467\\&\\&x_3=-1.380277569097618\\&\\&x_4=-1.380277569097614\\&\\&x_5=-1.380277569097614\\&\\&\text{Ya se ha repetido la solución luego es esa}\\&\\&------------\\&\\&\text{Y con }x_0=0.8\text{ hacemos lo mismo}\\&\\&x_1=0.8192818494835219\\&\\&x_2=0.8191725172066712\\&\\&x_3=0.8191725133961645\\&\\&x_4=0.8191725133961645\\&\\&\text{Y ya se repite, luego es es la otra solución}\end{align}$$

Luego las soluciones son

x = -1.380277569097614

x = 0.8191725133961645

·

Y eso es todo.