Como demuestro que triángulos semejantes tienen triángulos de Morley semejantes

·

Si usamos el teorema de Morley no es necesario nada. Como el teorema dice que el triángulo de Morley de cualquier triángulo es equilatero, entonces todos los triángulos de Morley son semejantes porque todos los triángulos equiláteros son semejantes.

Luego si se puede usar el toerema ya está.

·

Si no sepuede usar haremos una comprobación. No has usado una notación muy lógica, en el dibujo he usado otra.

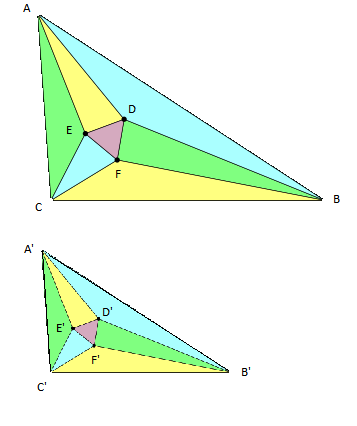
El ángulo en A y en A' es el mismo, luego su tercera parte es la misma. Lo mismo sucede en B y B'. Luego los triángulos ABD y A'B'D' son semejantes porque tienen los tres ángulos iguales

Y también la tercera parte del ángulo en C es igual a la tercera parte del ángulo en C', y se deduce que los triángulos ACE y A'C'E' son semejantes.

Esa semejanzas implican

AD/AB = A'D'/A'B'  ==> AD/A'D'  = AB/A'B'

AE/AC = A'E'/A'C'   ==> AE/AE'  = AC/A'C'

Y como ABC y A'B'C' son semejantes por hipótesis entonces

AB/A'B' = AC/A'C'

luego concluimos

AD/A'D' = AE/A'E' 

Y entonces en los triángulos ADE y A'D'E' tenemos dos lados semejantes y el ángulo entre ellos también los es por ser la tercera parte de un mismo ángulo.

Luego ADE y A'D'E' son semejantes

DE / D'E' = AD / A'D' = AB / A'B'

DE / D'E' = AB / A'B'

·

Haciendo razonamientos análogos sobre el vértice B llegarás a:

DF / D'F' = BC / B'C'

Y haciédolos sobre el vértice C se llega a

EF / E'F' = AC / A'C'

Por ser semejantes ABC y A'B'C' los miembro de la derecha de las tres conclusiones son iguales, luego los tres de la izquierda también lo son

DE / D'E' = DF / D'F' = EF / E'F'

Luego los triángulos DEF y D'E'F' son semejantes.

·

Y eso es todo.