Como podría hacer este ejercicio?

·

Las imágenes de la base canónica puestas como columnas nos dan la matiz de la aplicación lineal, así que la matriz es

( 0 1 -1)(-1 2 -1)( 1 -1 2)                                        ·Los valores propios los calcularemos así| 0-x   1    -1||-1    2-x   -1| = 0 | 1    -1   2-x|                                         ·-x(2-x)(2-x)-1-1+2-x+2-x+x = 0-x(2-x)(2-x) +2-x = 0(2-x)[-x(2-x)+1]= 0(2-x)(x^2-2x+1)=0(2-x)(x-1)^2 = 0

Luego hay dos valores propios, el valor propio 2 con multiplicidad 1 y el valor propio 1 con multiplicidad 2.

·

Yo no sé como os habrán dado la teoría a vosotros. Pero para mi el proceso de averiguar si es diagonalizable se hace calculando los vectores propios de los valores con multiplicidad mayor de 1, luego casi deberían ser las preguntas al revés. Si me pasas el libro de teoríame vendría bien.

Entonces voy a encontrar primero los autovectores, para ello hay que resolver los sistemas de ecuaciones como el del determinante de arriba cambiando la x por el valor propio correspondiente.

Para el valor propio 2 se resuelve este sistema

 0-2   1    -1 | 0-1    2-2   -1 | 0  1    -1   2-2 | 0                                 · 0   1  -1 | 0-1   0  -1 | 0 1 -1 0 | 0

Y este es uno de esos sistemas que no se resuelve por Gauss rápidamente pero por la segunda obtienes z=-x y por la tercera y=x

Luego tomando x=1 tendrás el vector propio (1,1,-1)

·

Y para el espacio propio del valor propio 1 resolvemos

 0-1 1 -1 | 0-1 2-1 -1 | 0 1 -1 2-1 | 0 · -1 1 -1 | 0 -1 1 -1 | 0 1 -1 1 | 0

Las tres son equivalentes luego la respuesta depende de dos parámetros

x=t

y=s

z=-t+s

(x,y,z) = t(1,0,-1) + s(0,1,1)

Luego el subespacio propio del valor propio 1 tiene dimensión 2 y estos son sus valores propios

{(1,0,-1),  (0,1,1)}

Y como la multiplicidad de los valores propios coincide con la dimensión de sus subespacios propios la matriz es diagonalizable

·

La matriz de paso P es la que se obtiene poniendo los vectores propios en columnas

 ( 1 1 0)P = ( 1 0 1) (-1 -1 1)

Y aquí esta comprobado con Máxima que es diagonalizable:

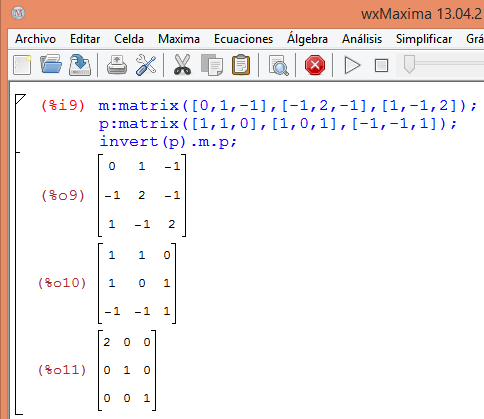
Y eso es todo.

gracias por tu ayuda Valero!

No hay nada más deprimente que cuando la página esta quita por su cuenta los saltos de línea y toda tabla o matriz queda hecha una braga. Voy a ver si puedo rehacerlas.

La del cálculo de valores propios

( 0 1 -1)(-1 2 -1)( 1 -1 2)                                        ·Los valores propios los calcularemos así| 0-x   1    -1||-1    2-x   -1| = 0 | 1    -1   2-x|                                         ·-x(2-x)(2-x)-1-1+2-x+2-x+x = 0-x(2-x)(2-x) +2-x = 0(2-x)[-x(2-x)+1]= 0(2-x)(x^2-2x+1)=0(2-x)(x-1)^2 = 0

La del cálculo del espacio propio de 2

 0-2   1    -1 | 0-1    2-2   -1 | 0  1    -1   2-2 | 0                                                                              ·  0   1  -1 | 0-1   0  -1 | 0  1  -1   0 | 0

La del cáculo del espacio propio de 1

0-1    1    -1 | 0-1    2-1   -1 | 0  1    -1   2-1 | 0                                 · -1   1  -1 | 0 -1   1  -1 | 0   1 -1 1 | 0

Espero que ahora se vea. Todo son inconvenientes para los matemáticos en esta página.

1) Ponen un inmenso espacio entre párrafos, por lo que si escribes las matrices en escritura normal quedan muy separadas las filas.

2) No funciona bien el LaTeX con las matrices, luego no se puede usar el editor de ecuaciones con ellas.

3) Cuando le da la gana se quitan los saltos de línea en los bloques de código y pasa lo que ha pasado.

4) No podemos escribir las variables x, k, q, s, d enseguida está el editor diciendo que somos humanos y hemos fallado y nos propone el cambio por "por", "que", "que", "es", "de". Prefiero ser humano y errar como humano que ser máquina y fallar como máquina.

·

Bueno, ojalá se vean bien ahora los bloques de texto.

Nada, no hay forma.