Como podría hacer este ejercicio de diagonalización
Estudie para qué valores del parámetro a es diagonalizable la aplicación lineal de matriz asociada
2 Respuestas
Tienes dos formas de resolverlo (que por supuesto son equivalentes).
1) Diagonalizando la matriz
/ 2 1 0 \
| 0 a 0 |
\ 3 6 1 /
F3 = 2F3 - 3F1
/ 2 1 0 \
| 0 a 0 |
\ 0 9 2 /
F3 = aF3 - 9F2
/ 2 1 0 \
| 0 a 0 |
\ 0 0 2a /
Para que sea diagonal, tanto a como 2a deben ser distinto de cero por lo que llegás a la conclusión que a debe ser distinto de cero.
La otra forma de verificar esto (y en este caso mucho más sencillo es calcular el determinante y pedir que sea distinto de cero.
Calculo el determinante, expandiendo por la tercer columna
0 * det(0 6 - 3a) - 0 * det (2 6 - 3 1) + 1 * det (2 a - 0 1)=
=det (2a-0) = 2a
Como debe ser distinto de cero, entonces a distinto de cero
·
Diagonalizable no significa que con operaciones de fila se pueda obtener una matriz diagonal sin ceros en la diagonal. Eso lo cumplen todas las que tienen determinante distinto de cero.
Diagonalizable significa ser una matriz semejante a una matriz diagonal D, es decir que existe otra matriz P tal que
P^(-1)·M·P = D
Y como bien sabes, para determinar si una matriz es diagonalizable es posible que tengas que hacer muchas cuentas.
Primeramente se calculan los valores propios
|2-x 1 0 | | 0 a-x 0 | = 0 | 3 6 1-x| · (2-x)(a-x)(1-x) = 0
¡Uff, qué facil ha salido, menos mal!
Los valores propios son 1,2, y a
Si a es distinta de 1 y de 2 ya es diagonalizable, toda matriz con valores propios de multiplicidad 1 es diagonalizable.
Y ahora sería cuestión de estudiar aparte los casos a=1 y a=2. La matriz será diagonalizable si el espacio propio correspondiente tiene dimensión 2.
Para a=1 el espacio propio del valor propio 1 se calcula así
1 1 0 | 0
0 0 0 | 0
3 6 0 | 0
Hay dos ecuaciones independientes luego el subespacio propio tiene dimensión 3-2 = 1 NO es diagonalizable
Para a=2 el espacio propio del valor propio 2 se calcula así
0 1 0 | 0
0 0 0 | 0
3 6 -1 | 0
De nuevo hay dos ecuaciones independientes y por lo tanto la dimensión del espacio propio es 1 que es distinta de la multiplicidad del valor propio y por lo tanto no es diagonalizable.
·
Luego la respuesta es la que ya se dio hace tiempo. Es diagonalizable para
$$\begin{align}&a\in \mathbb R-\{1,\;2\}\end{align}$$·
Aunque no lo piden se puede calcular la matriz de paso
2-x 1 0 | 0 0 a-x 0 | 0 3 6 1-x| 0 · Para el valor propio 1 1 1 0 | 0 0 a-1 0 | 0 3 6 0 | 0 Por ejemplo tomamos el vector (0,0,1) · Para el valor propio 2 0 1 0 | 0 0 a-2 0 | 0 3 6 -1 | 0 Tomamos por ejemplo (1, 0, 3) · Y para el valor propio a distinto de 1 y 2 2-a 1 0 | 0 0 0 0 | 0 3 6 1-a| 0 · y=(a-2)x 3x + 6x(a-2) +(1-a)z = 0 z=[-3x-6x(a-2)]/(1-a)= (9-6a)x/(1-a) podemos tomar (1, a-2, (9-6a)/(1-a))
Y la matriz de paso será
$$\begin{pmatrix}0&1&1\\0&0&a-2\\1&3&\frac{9-6a}{1-a}\end{pmatrix}$$Como es fácil haberse equivocado, voy a comprobarlo con Maxima
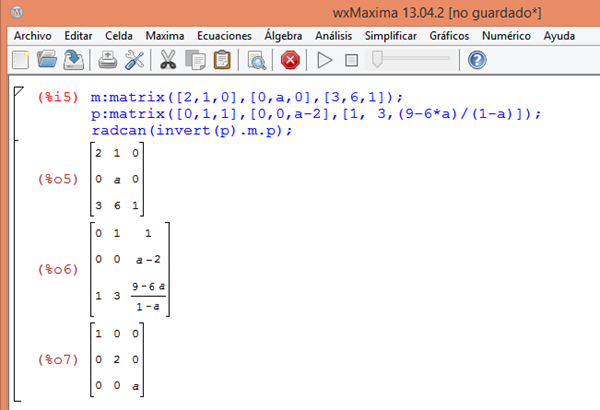
Luego está bien, el producto de las tres matrices da la matriza diagonal de los valores propios. Incluso intercambiando las filas de P podriamos haber hecho que la diagonal fuera (2, a, 1) que es más similar a la matriz que nos dan, pero eso no es obligatorio y así está igualmente bien.
Y eso es todo.