Como obtener la ecuación de una hipérbola que tiene sus vértices en ±(3, 0) y pasa por el punto P(5, 2).

De los Vértices vemos que la hipérbola tiene su centro en el origen de coordenadas y el eje mayor en el eje OX. Luego su ecuación será del tipo:

$$\begin{align}&\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\\&\\&a=3\\&\\&\frac{x^2}{3^2}-\frac{y^2}{b^2}=1\\&\\&pasa \ por \ P=(5,2)\\&\Rightarrow\\&\frac{5^2}{3^2}-\frac{2^2}{b^2}=1\\&\\&25b^2-36=9b^2\\&16b^2=36\\&b^2=\frac{36}{16}\\&\\&b=\frac{6}{4}=\frac{3}{2}\\&a)\\&\frac{x^2}{3^2}-\frac{y^2}{(\frac{3}{2})^2}=1\\&\\&Focos:\\&c^2=a^2+b^2=3^2+(\frac{3}{2})^2=\frac{45}{4}\\&\\&c=\pm \frac{3 \sqrt{5}}{2}\\&F=(+\frac{3 \sqrt{5}}{2},0)\\&\\&F'=(-\frac{3 \sqrt{5}}{2},0)\\&\\&Asíntotas:\\&y=\pm \frac{b}{a}x\\&\\&\frac{b}{a}=\frac{\pm \frac{3}{2}}{3}=\pm \frac{1}{2}\\&\\&y=\pm \frac{1}{2}x\end{align}$$

Graficando:

·

Los vértices son (-3,0) y (3,0), el centro es siempre el punto medio entre los vértices

(1/2) · [(-3,0)+(3,0)]/2 = (1/2) · (0,0) = (0,0)

·

Cuando el eje transversal (el de los focos) es paralelo al eje X, la distancia del centro al vértice es el parámetro a de la hipérbola y la ecuación canónica es

$$\begin{align}&\frac {x^2}{3^2}-\frac{y^2}{b^2}=1\\&\\&\text{Al pasar por (5,2)}\\&\\&\frac {5^2}{9}-\frac{2^2}{b^2}=1\\&\\&\text{multiplicamos por }9b^2\\&\\&25b^2-36=9b^2\\&\\&16b^2= 36\\&\\&b^2={{36}\over{16}}={9 \over 4}\\&\\&\text{Luego la ecuación es}\end{align}$$

Está dando problemas el editor de ecuaciones, no sé si podré continuar.

$$\begin{align}&\frac {x^2}{3^2}-\frac{y^2}{\left(\frac 32  \right)^2}=1\\&\\&\\&\text{Las asíntotas tienen pendiente }\pm \frac ba\\&\\&\text {Y pasan por el centro}\\&\\&y=\pm \frac{\frac 32}{3}x +k=\pm \frac x2+k\\&\\&\text{por pasar por (0,0)}\\&\\&0=0+k\implies k=0\\&\\&\text{Las asíntotas son:}\\&\\&y=\frac x2\\&y=-\frac x2\\&\\&\text{La distancia focal en la hipérbola es}\\&\\&c= \sqrt{a^2+b^2}=\sqrt{9+\frac 94}=\frac {\sqrt{45}}2=\frac 32 \sqrt 5\\&\\&\text{Y los focos equidistantes del centro en el eje transversal son}\\&\\&\left(-\frac 32 \sqrt 5,\;0  \right)\quad y \quad \left(\frac 32 \sqrt 5,\;0  \right)\end{align}$$

Y esta es la gráfica:

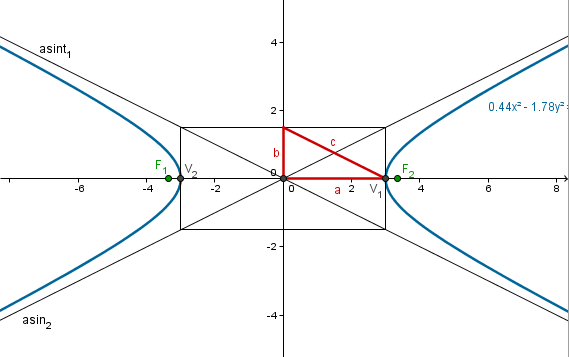
Y eso es todo.