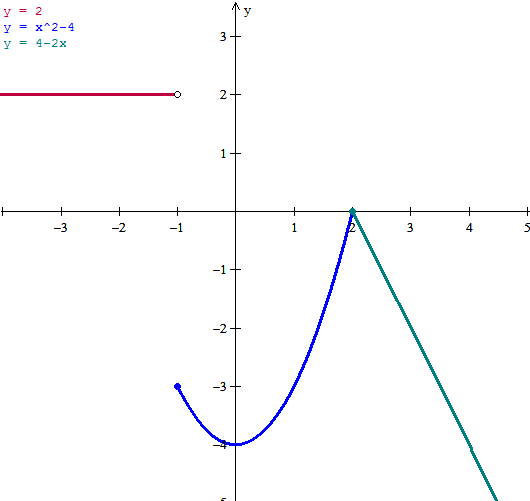Cómo representar las siguientes funciones?
Representar gráficamente las siguientes funciones indicando su dominio, imagen, monotonía, extremos. Asíntotas y cortes con los ejes:
1 Respuesta
·
Son muchos ejercicios, cada pregunta debería llevar un solo ejercicio a no ser que sena muy sencillos y cortos. Haré el primero y los otros mándalos en nuevas preguntas de uno en uno.
1) Todos los trozos son polinomios luego no hay ningún problema de puntos donde no estén definidos. Y la unión de los dominios de cada trozo es R, luego
Dom f = R
·
La imagen del primer trozo es {2}
El segundo trozo tiene máximos y mínimos absolutos e elegir entre el valor en los extremos y el valor en los puntos críticos, la derivada es
y'=2x
el valor crítico es 0
f(-1) = (-1)^2 - 4 = -3
f(0) = 0^2 - 4 = -4
f(2) = 2^2 - 4 = 0
La imagen del segundo trozo es [-4, 0)
La imagen del tercer trozo es la una semirecta decreciente cuyo punto más alto es el inicial
f(2) = 4 - 2·2 = 0
Luego es (-infinito, 0]
Luego la imagen de la función es la unión de las imagenes de los tres trozos y es
Im f = (-infinito, 0] U {2}
·
Monotonía
En el primer trozo la función es constante, no es ni monotona creciente ni decreciente.
En el segundo la derivada es
f'(x) = -2x
Luego es decreciente en (-1, 0) y creciente en (0,2)
En el tercer trozo es siempre decreciente, es una recta con pendiente negativa o lo puedes comprobar también con la derivada
f'(x)=-2
Lo resumimos todo
(-Infinito, -1) constante
(-1, 0) decreciente
(0, 2) creciente
(2, infinito) decreciente
·
Los extremos sugen de los valores en los límites de los intervalos o en los puntos críticos. Entendiendo por puntos críticos tanto los puntos donde la derivada es 0 como aquellos donde no es derivable. Siendo una función por trozos el trabajo se multiplica
En -(infinito,-1) f(x) = 2
En -1 f(-1)=(-1)^2-4 = -3 y después decrece hasta -4
En 0 f(0)= 0^2 - 4 = -4 y después crece hasta 0
en 2 f(2) = 4-2x = 0 y después decrece hasta - infinito
Y los extremos son
Máximo absoluto f(x)=2 en (-infinito, -1)
Mínimo absoluto, no existe, tiende a -infinito
Máximos relativos:
En sentido estricto solo sería f(2)= 0
En sentido no estricto se puede añadir f(x)=2 en (-infinito,-1)
Mínimos relativos:
En sentido estricto solo sería f(0) = -4
En sentido no estricto se puede añadir f(x)=2 en (-infinito,-1)
·
Asíntotas:
Tiene una asíntota horizontal en - infinito
y=2
Tiene una asíntota oblicua en + infinito
y=4-2x
·
Los cortes con los ejes son:
Eje X:
Trozo izquierdo no corta
Trozo intermedio
x^2-4=0
x^2 = 4
x = -2 y 2
pero no pertenecen al dominio [-1, 2) del trozo intermedio, luego nada
Trozo derecho
4-2x=0
2x=4
x=2
que pertenece al dominio del trozo derecho [2, +infinito)
Luego los cortes con el eje X son {(2,0)}
·
El corte con el eje Y es el valor de la función en x=0 para ello se tiene que tomar el trozo segundo
f(0) = 0^2-4 = -4
Luego el corte con el eje Y es (0, -4).
·
Y finalmente la gráfica para corroborar todo.
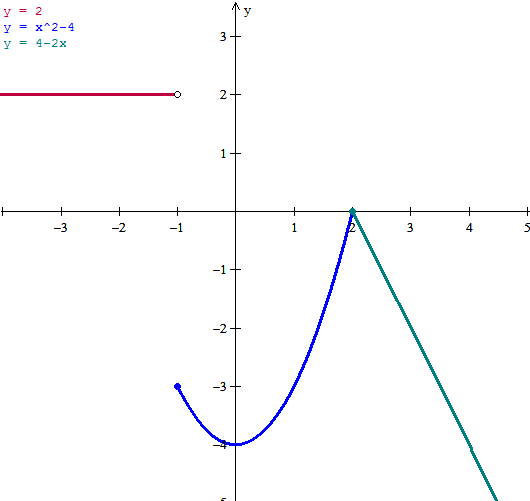
Y eso es todo.
Muchas gracias!! ya los he subido de uno en uno para poder entenderlos mejor,porque si no se me hace un poco más lioso
Tienes razón son todos demasiado largos para hacerlos en una sola pregunta
Gracias de nuevo!!
Mery!
El trabajo hecho ha sido mucho. Esto merece una puntuación de Excelente. Y si no lo merece, dejaré de contestar tus preguntas porque es imposible hacerlo mejor y por lo tanto sería imposible obtener la puntuación que se merece.
Ahora mismo pensaba contestar las otras tres preguntas que has mandado, pero no lo haré mientras no subas la nota de esta.
