Calcule el menor punto critico positivo de F(x)=ln(cosh(x))+ln(cos(x))

Veamos...

Como no parece una función "sencilla", primero la voy a graficar para ver si esto nos ayuda (se que no podrás hacerlo en el examen, pero al menos ahora nos dará una idea de lo que necesitamos...)

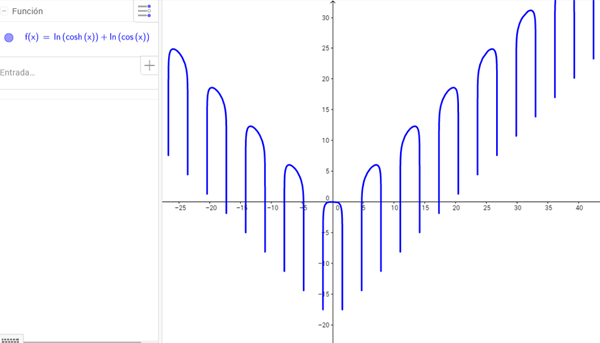
Por lo que podemos ver de la imagen, parecería que la derivada cercana al cero es cero, por lo que ese será su menor punto crítico positivo

Intentemos analizar un poco la función y la derivada...

$$\begin{align}&f(x) = ln(cosh(x)) + ln(\cos(x))\\&f'(x)=\frac{1}{cosh(x)}sinh(x)+\frac{1}{\cos(x)}(-\sin(x))\\&f'(x)=tanh(x) - tan(x)\\&f'(x)=0 \to 0=tanh(x)-tan(x) \to\\&\frac{e^x+e^{-x}}{e^x-e^{-x}}=\frac{\sin(x)}{\cos(x)} \text{   (escribo las tangentes de esa forma para ver si puedo deducir algo)}\\&({e^x+e^{-x}}){\cos(x)} ={\sin(x)}({e^x-e^{-x}})\\&\text{Hagamos algunas cuentas, aunque no se si vamos a llegar a algo...}\\&e^x \cos(x)+e^{-x}\cos(x) =\sin(x)e^x-\sin(x)e^{-x}\\&e^{-x}\cos(x)+\sin(x)e^{-x} =\sin(x)e^x-e^x \cos(x)\\&e^{-x}(\cos(x)+\sin(x)) =e^x(\sin(x)-\cos(x))\\&\frac{(\cos(x)+\sin(x))}{(\sin(x)-\cos(x))} =\frac{e^x}{e^{-x}}\\&\frac{(\cos(x)+\sin(x))}{(\sin(x)-\cos(x))} \cdot \frac{(\cos(x)+\sin(x))}{(\sin(x)+\cos(x))} =(e^x)^2\\&\frac{\cos^2(x)+\sin^2(x)+2cos(x)\sin(x)}{(\sin^2(x)-\cos^2(x))} =(e^x)^2\\&\frac{1+2cos(x)\sin(x)}{(\sin^2(x)-(1-\sin^2(x))} =(e^x)^2\\&\frac{1+\sin(2x)}{(2sin^2(x)-1)} =(e^x)^2\\&\text{Y la verdad que pese a haber llegado a expresiones interesantes, no veo que sea fácil encontrar}\\&\text{el valor de x que iguala esa expresión, por lo que creo que esto no se puede resolver análiticamente, sino}\\&\text{que hay que recurrir a otros métodos como, por ejemplo, el método de Newton-Raphson}\end{align}$$

Y hasta ahí pude llegar, salvo que pasemos a métodos de resolución que no sean analíticos, no encuentro la forma de resolverlo :(

HOla nosotros estamos trabajando con newton

Ok, los puntos críticos sabemos que será cuando f'(x)=0 (y debemos quedarnos con el primer valor positivo)

Así que vamos a considerar f'(x) como la nueva función (digamos g(x)) y para calcular Newton necesitamos calcular g'(x).

$$\begin{align}&f'(x)=g(x)=tanh(x)-tan(x)\\&\text{Como vamos a derivar, conviene poner los términos en que se compone las tangentes}\\&g(x)=\frac{e^x+e^{-x}}{e^x-e^{-x}}-\frac{\sin(x)}{\cos(x)}\\&g'(x)= 1-tanh^2(x)-(1+tan^2(x))\\&g'(x)=-(tanh^2(x)+tan^2(x))\\&\text{El método de N-R dice}\\&x_{n+1}=x_n - \frac{g(x)}{g'(x)}\\&x_{n+1}=x_n - \frac{tanh(x)-tan(x)}{-(tanh^2(x)+tan^2(x))}\\&x_{n+1}=x_n + \frac{tanh(x)-tan(x)}{(tanh^2(x)+tan^2(x))}\end{align}$$

y a partir de ahí creo que ya puedes seguirlo con las iteraciones (ojo con los valores iniciales que usas y la precisión que necesitas)

·

Hacemos todo lo que hizo Gustavo, como yo he aplicado la versión con secantes de a derivada llego a

$$\begin{align}&x_{n+1}=x_n-\frac{tanh\,x_n-tg\,x}{sech\,x_n-sec\,x}\end{align}$$

Entonces lo fundamental es empezar con un valor cercano a la respuesta.  Por la gráfica pudes ver que la derivada cero del primer arco de la derecha está más o menos por el 7, tomaremos ese número como x_0

Y los resultados son

x_1 = 7.07306412415216

x_2 = 7.06860288827473

x_3 = 7.06858274603447

x_4 = 7.06858274562874

x_5 = 7.06858274562874

Ya se repite, luego esa es la solución.

·

Y eso es todo, no olvides valorar las respuestas.

Lo que sucede en el cero es que la función es tan plana, tan plana, que el método de Newton no converge, la tangente en un punto te lleva a otro relativamente muy lejano y el método se queda por los alrededores sin llegar al 0, pero la única raíz de los alrededores es 0, hasta la que he dicho yo no hay otra.