Demuestra que si las diagonales de un cuadrilátero se bisectan entre sí, entonces los lados opuestos son paralelos.
En la siguiente imagen demostrar que si
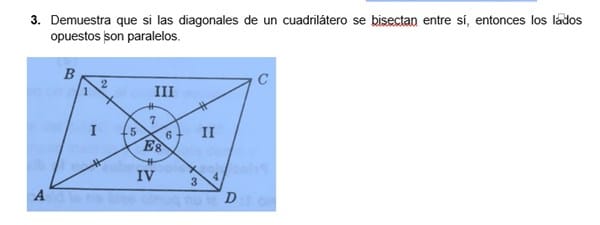
Las diagonales de un cuadrilátero se bisectan entre sí, entonces los lados opuestos son paralelos.
Esta es la respuesta al problema planteado.
∢ AEB ≅ ∢ CED. Los ángulos opuestos por el vértice son congruentes.
∆ AEB ≅ ∆ CED. Si dos lados y el ángulo entre ellos son congruentes, los dos triángulos son congruentes.
(AB)̅≅(CD)̅ Los lados correspondientes de triángulos congruentes, son también congruentes
∢AED ≅ ∢BEC Los ángulos opuestos por el vértice son congruentes.
∆ AED ≅ ∆ BEC Si dos lados y el ángulo entre ellos son congruentes, los dos triángulos son congruentes.
(AD)̅≅(BC)̅ Los lados correspondientes de triángulos congruentes, son también congruentes
ABCD Si dos pares de lados opuestos de un cuadrilátero son congruentes, la figura es un paralelogramo.
1 respuesta más de otro experto
--
--
Hola Francisco:
La demostración de que los triangulos opuestos por un vértice son congruentes y por tanto los lados laterales miden lo mismo dos a dos está bien. Pero tienes que demostrar que son paralelos. Para ello tendrás que hacer un poco de cuentas con los ángulos en los vértices para ver que el ángulo BAD es congruente con el CDF, donde F es un punto a la derecha sobre la recta AD. Con ello AB será paralelo a CD. Y lo mismo tendr´sque hcer con BAD y GBC, donde G esta sobre AB y es superior a B para demostrar que BC es paralelo a AD.
Y eo es todo. Saludos.
--
--