Hallar los ceros , las coordenadas del vértice ..

Son muchos ejercicios para una sola pregunta. Haré el primero y tendrás que esperar que otro experto te responda los otros, o plantear nuevas preguntas

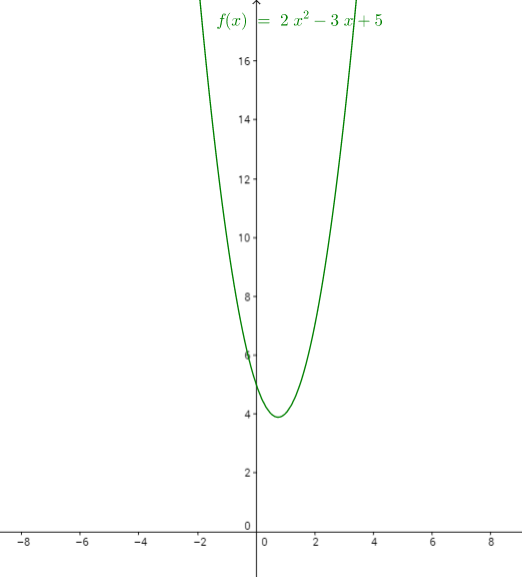
f(x)=2x^2-3x+5

$$\begin{align}&f(x)=2x^2-3x+5\\&Ceros:\\&x_{1,2}=\frac{3 \pm \sqrt{(-3)^2-4 \cdot 2 \cdot 5}}{2\cdot2}=\frac{3 \pm \sqrt{-31}}{4}\\&x_1=\frac{3}{4} + i \frac{\sqrt{31}}{4}\approx 0.75 + i \ 1.391941\\&x_2=\frac{3}{4} - i \frac{\sqrt{31}}{4}\approx 0.75 - i \ 1.391941\\&\text{Las coordenadas del vértice están en el valor de x que es el promedio de las raíces o en punto x= b/2a}\\&x_{vertice}=\frac{x_1+x_2}{2}=\frac{\frac{3}{4} + i \frac{\sqrt{31}}{4}+\frac{3}{4} - i \frac{\sqrt{31}}{4}}{2}=\frac{3}{4}=0.75\\&y_{vertice}=\\&f(x_{vertice})=f(0.75)=2 \cdot (0.75)^2-3\cdot0.75+5=3.875\\&\text{Eje de simetría: } x=0.75\\& Crecimiento/Decrecimiento:\\&\text{es un polinomio cuyo coeficiente "a" es positivo, así que tiene las ramas hacia arriba, por lo tanto decrecerá }\\&\text{hasta el vértice y luego crecerá}\\&Crecimiento: (0.75, +\infty)\\&Decrecimiento: (-\infty, 0.75)\\&\text{No preguntás por los intervalos de positividad y negatividad, pero veamos}\\&Positividad: \text{Vimos que las raices son complejas y en el vértice es positiva, así que la función es positiva para todo R}\\&Negatividad: \text{Por lo mismo que antes, = } \emptyset\\&\end{align}$$

y la gráfica es