Matemáticas administrativas e ingresos marginales, determinar función
Alguien que me pueda ayudar por favor con este pequeño problema sobre ingresos marginales.
·
·
¡Hola Luis!
Los ingresos marginales son la derivada de los ingresos totales, luego los ingresos totales son la integral de los marginales.
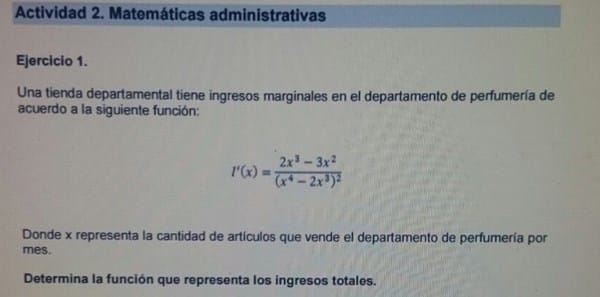
$$\begin{align}&IT(x)=\int I_{Marg}(x)dx=\\&\\&\int \frac{2x^3-3x^2}{(x^4-2x^3)^2}dx=\\&\\&\text{Si multiplicamos por 2 el numerador vemos}\\&\text{que tenemos la derivada del paréntesis del denominador}\\&\\&=\frac 12\int \frac{4x^3-6x^2}{(x^4-2x^3)^2}dx=\\&\\&\text{Esto es medio inmediato, si quieres haces el }\\&\text{cambio de variable pero no lo veo necesario}\\&\\&=-\frac 12 ·\frac{1}{x^4-2x^3}+C =-\frac{1}{2x^4-4x^3}+C\end{align}$$Y el que ha hecho este problema se ha lucido pero de lo lindo. La finción IT(x) resultante se parece a todo menos a una función de ingreso. ¿Dónde se ha visto que para 0 unidades el límite sea infinito? Debería ser una cantidad que pudiéramos arreglar con C para que valiese cero. Pero como el límite es infinito no se puede arreglar con ninguna constante que pongamos.
Luego a este problema podríamos llamarlo simplemente calcula la integral indefinida y dejar lo de que es una función de ingreso, no tiene solución
Saludos.
:
.
