Integrales indefinidas resolver paso apaso
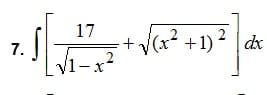
Buenas tardes si pueden resolver la integral y derivar para llegar la función original
Respuesta de Valero Angel Serrano Mercadal
1
1 respuesta más de otro experto
Respuesta de Lucas m
1
