Como resuelvo estos problemas de continuidad de una función vertical
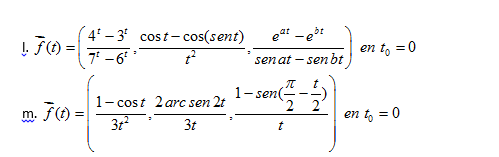
- Calcular los siguientes limites si existen
Ayúdenme con estos problemas de continuidad
2 respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
