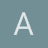¿Cómo puedo hallar la función de densidad del siguiente ejercicio?
Hola expertos, espero puedan apoyarme en este ejercicio para hallar la densidad de U y V.
1 respuesta
·
·
¡Hola Atom!
La función de densidad de una distribución uniforme es 1 entre la longitud del intervalo
f_x(x) = f_y(y) = 1/[2-(-1)] = 1/3
Y lo que realmente necesitas conocer es la fórmula para la función de densidad de la suma de dos variables continuas, es esta:
$$\begin{align}&\text{Primero calculamos la función de densidad de 2X}\\&\text{que se calcula así de fácil}\\&\\&f_{2X}(x)=\frac 16 \quad si -2\le x\le 4\\&\\&\text{y ahora calculaemos}\\&\\&f_U(u)=f_{2X+Y}(u)\\&\\&\text{U podrá tomar valores entre -3 y 6}\\&\text{Calculemos la función de densidad en subintervalos}\\&\\&Como \;u=y+2x\\&y=u-2x\\&Como\; 2x \in[-2,4]\\&y \in[u-4,u+2]\cap[-1,2]\\&\\&Si\; u\le 3\implies y>=-1\\&Si \;u>=0 \implies y\le 2\\&\\&También\\&2x=u-y\\&Como \;y\,\in[-1,2]\\&2x\in[u-2,u+1]\cap [-2,4]\\&\\&Si \;u\le0\implies 2x\ge-2\\&Si \;u \ge 3 \implies 2x\le4\\&\\&\text{Y separamos estos casos}\\&1)\; u\le0 \implies y\in[-1,u+2], \quad 2x\in[-2,u+1]\\&\\&f_U(u)=\frac 13·\frac 16(u+2-(-1)) =\frac {u+3}{18}\\&\\&2)\quad 0<=u<=3\implies y\in[-1,2],\quad 2x \in[u-2,u+1]\\&\\&f_U(u) = \frac 13·\frac 16·(2-(-1)) = \frac 16\\&\\&3) \quad3\le u\le6\implies y\in[u-4,2],\quad 2x \in[u-2,4]\\&\\&f_U(u)= \frac 13·\frac 16(6-u)=\frac{6-u}{18}\\&\\&\text{Y esa es la función de densidad en tres trozos}\\&\text{Vamos a verificar si su integral es 1}\\&\\&\int_{-3}^0 \frac{u+3}{18}du+\int_0^3 \frac {du}6+\int_3^6 \frac{6-u}{18}du=\\&\\&\frac 1{18}\left[\frac {u^2}{2}+3u \right]_{-3}^0+\frac 36+\frac 1{18}\left[6u-\frac{u^2}{2} \right]_3^6=\\&\\&\frac 1{18}\left(-\frac 92+9 \right)+\frac 12+\frac 1{18}\left(36-18-18+\frac 92 \right)=\\&\\&\frac 1{18}·\frac 92+\frac 12+\frac 1{18}·\frac 92=\frac 14+\frac 12+\frac 14=1\end{align}$$Luego está bien.
Yo no sé como te lo habrán enseñado y es la primera vez que hago uno de estos y me es difícil explicarte por qué he hecho esas cosas pero son esas cosas.
Por supuesto que semejante ejercicio solo se puede hacer uno por pregunta.
Saludos.
:
:
¡Gracias! Señor Valero. Por cierto ¿le puedo mandar el inciso b en otra pregunta?
Si, mándalo. Pero no te garantizo cuando lo pueda responder, es un problema complicado aunque una vez que aprendí como se resuelve el primero a lo mejor ya no me cuesta tanto.
Saludos.
:
:
