Anónimo
¿ Problema sobre región comprendida,como resolver?
Integrales.
2 Respuestas
En realidad, el resultado es incorrecto, ya que se ha tenido un fallo al momento de dar con la ecuación de la recta que pasa por los puntos dados.
la ecuación de la recta sería: y= 2x-2.
Y resolviendo con el mismo procedimiento anterior el resultado final es: 36.
·
·
¡Hola Anónimo!
Haré la gráfica pero se podría deducir todo sin hacerla.
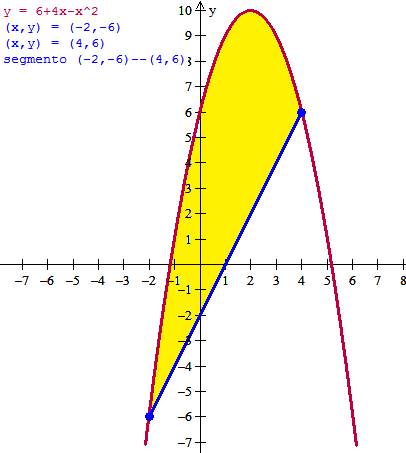
Es que tenía el temor de que la cuerda no fuera verdadera y en vez de comprobar si los puntos perteneciían a la parábola he aprovechado para dibujarlo todo.
Necesitaremos conocer la función azul. Es una recta pasando por dos puntos
y = yo + m(x-xo)
donde m es la pendiente que es
m=(y1-y0)/(x1-x0)=[6-(-6)] / [4-(-2)] = 12/6=2
y = -6+2[x-(-2)]
y = -6 + 2x +4
y = 2x+2
Te dejo que compruebes analíticamente que los puntos que nos dan peretenecen a la parábola. Luego la ecuación que quedaria para calcular los puntos de intersección recta parabola es de grado 2
2x+2 = 6+4x-x^2
Luego solo puede tener dos soluciones que son las que nos dan. Por lo tanto las dos funciones no se cruzan más veces y por tanto el área se puede calcular toda de golpe sin dividir el dominio de integración. Y finalmente, al ser la parábola hacia abajo por tener coeficiente director negativo, la cuerda estará por debajo entre los dos puntos de corte.
Todo esto que he hecho puede parecer excesivo pero es lo que habría que hacer. Y con todo eso se ha llegado a la conclusión de que el área es:
$$\begin{align}&a=\int_{-2}^4[(6+4x-x^2)-(2x+2)]dx=\\&\\&\int_{-2}^4(-x^2+2x+4)dx=\\&\\&\left[-\frac{x^3}{3}+x^2+4x \right]_{-2}^4=\\&\\&-\frac {64}3+16+16-\frac 83-4+8=-\frac {72}3+36=\\&\\&-24+36=12\end{align}$$:
:
En efecto hice mal un paso, lo correcto es
y = -6 + 2x +4
y = 2x-2
y el área es:
$$\begin{align}&a=\int_{-2}^4[(6+4x-x^2)-(2x-2)]dx=\\&\\&\int_{-2}^4(-x^2+2x+8)dx=\\&\\&\left[-\frac{x^3}{3}+x^2+8x \right]_{-2}^4=\\&\\&-\frac {64}3+16+32-\frac 83-4+16=-\frac {72}3+60=\\&\\&-24+60=36\end{align}$$Perdón por el fallo.
Saludos.
:
: