Como hallar el punto medio del segmento AB?
Se consideran los puntos A,B y C afijos a=2+3i ,B=4-i y C=5+2i
1) Halla el punto medio I , del segmento [AB].
2) calcula (a-c)/(b-c) en forma binomica y polar.
3) Deduce la naturaleza del triángulo ABC.
1 Respuesta
Respuesta de Lucas m
1
;)
Hola Sia!
a) Afijos:
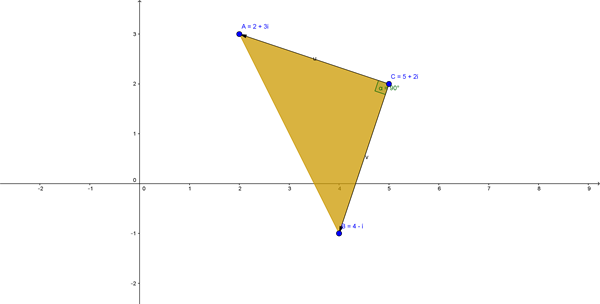
A=(2,3) ; B=(4,-1) ; C=(5,2)
a) I=(A+B)/2=(3,1)
b)
$$\begin{align}&A-C=2+3i-(5+2i)=-3+i\\&\\&|-3+i|=\sqrt{3^2+1^2}=\sqrt {10}\\&tan \ \alpha=\frac{1}{-3} \\&\alpha=arctan(\frac{1}{-3})=2ºcuadrante=161º33'54''\\&\\&B-C=4-i-(5+2i)=-1-3i\\&\\&|-1-3i|=\sqrt{1^2+3^2}=\sqrt {10}\\&\\&tan \beta=\frac{-3}{-1}=3rquadrante \\& \beta=arctan3=71º33'54''+180º=251º33'54''\\&\\&\frac{A-C}{B-C}=\frac{ \sqrt {10}_{161º33'54''}}{\sqrt {10}_{251º33´54''}}=1_{-90º}=1_{270º}\\&\\&\frac{A-C}{B-C}=\frac{-3+i}{-1-3i}=\frac{-3+i}{-1-3i}\frac{-1+3i}{-1+3i}=\\&\\&=\frac{3-9i-i+3i^2}{1-9i^2}=\frac{-10i}{10}=-i\\&\\&c)\\&\frac{A-C}{B-C}=\frac{\vec{CA}}{\vec{CB}}=1_{-90º}\\&\\&\vec{CA}=1_{-90º}·\vec{CB}\\&\\&Giro \ 90º \ sentido \ contrario \ manecillas \ reloj \\&y \ modulo \ 1\end{align}$$ABC es un triángulo rectángulo isósceles
;)
;)
