Quien sabe sobre Graficar los 5 primeros términos de las siguientes progresiones
Graficar los 5 primeros términos de las siguientes progresiones y determinar para cada progresión si es geométrica o aritmética, su razón o diferencia común y si es creciente o decreciente.
a) 𝑈𝑛=2𝑛−3
b) 𝑈𝑛=8−2𝑛
c) 𝑈𝑛=2𝑛−1
d) 𝑈𝑛=−3𝑛−1
1 respuesta
·
·
¡Hola Isa!
Me temo que aquí no nos vamos a entender, estoy seguro que muchas expresiones no son lo que se ve y es imposible adivinarlas
Yo veo
Un = 2n-1
pero no sé si te refieres a
Un = (2·n)-1
Un = (2^n) - 1
Un = 2^(n-1)
Ya me pasado con varios ejercicios que no escriben las expresiones de forma adecuada.
Deberías explicar bien com es cada una de las sucesiones, bien con lenguaje de símbolos sin faltar ningún paréntesisi o dicho de palabra.
Saludos.
:
:
Así están en la hoja que nos dio profesor así tal cual los escribí cada ejercicio
Si están bien escritos así son todas aritméticas, por eso me extrañaba la pregunta.
Sobre lo de gráficar querrán decir graficar imagino, en un sistema de ejes cartesiano.
Vamos primero a calcular los 5 primeros términos
a) Un = 2n-3
El primer término es U1 y se obtiene haciendo n=1, luego
U1 = 2·1 - 3 = 2-3 = -1
el segundo se obtiene haciendo n=2
U2 = 2·2 - 3 = 4-3 = 1
U3 = 2·3 - 3 = 6-3 = 3
U4 = 2·4 - 3 = 8-3 = 5
U5 = 2·5 - 3 = 10-3 = 7
·
b) Un = 8 - 2 n
Calculamos U1 con n=1
U1 = 8-2·1 = 8 - 2 = 6
U2 = 8 - 2·2 = 8-4 = 4
Como son artiméticas sabemos que la diferencia es constante, entonces en vez de hacer tantas cuentas sumamos o restamos la diferencia y vamos sacando los términos uno tras otro
U3 = U2 - 2 = 2
U4 = 2 -2 = 0
U5 = 0 - 2 = -2
Y con las c) y d) se hace igual.
Vas a tener estos puntos:
a) -1, 1, 3, 5, 7 es aritmética, la diferencia es 2 y es creciente
b) 6, 4, 2, 0, -2 es aritmética, la diferencia es (-2) y es decreciente
c) 1, 3, 5, 7, 9 es aritmética, la diferencia es 2 y es creciente
d) -4, -7, -10, -13, -16 aritmética, diferencia (-3) y decreciente
Y la gráfica es esta, espero que sea lo que pedían:
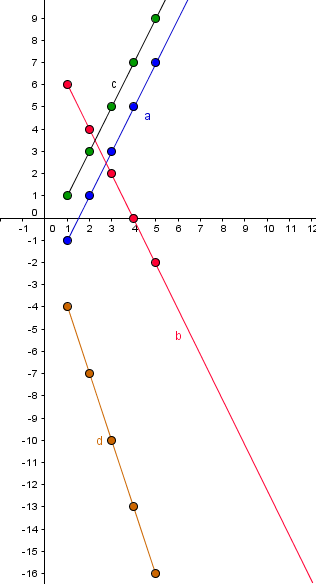
Y eso es todo, saludos.
:
:
La C y la D son progresiones geometricas - Daniela Agudelo Perez