En la siguiente actividad consiste en determinar la transformada de Laplace de la siguiente función 5/6
Determinar la transformada de Laplace de la función
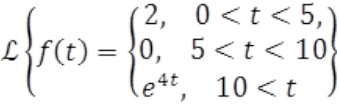
Indicando los pasos hasta llegar a la solución de la transformada de Laplace .
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
Usaré la definición de transformada de Laplace.
$$\begin{align}&\mathcal L\{f(t)\mathcal\}=\int_0^{\infty}e^{-st}f(t)dt=\\&\\&\text{La divido en los trozos que tiene}\\&\\&=\int_0^{5}e^{-st}·2\;dt+\int_5^{10}e^{-st}·0dt+\int_0^{\infty}e^{-st}e^{4t}dt=\\&\\&2\int_0^{5}e^{-st}\;dt+0+\int_0^{\infty}e^{(4-s)t}dt=\\&\\&-\frac 2s·e^{-st}\bigg|_0^5+\frac 1{4-s}e^{(4-s)t}\bigg|_{10}^{\infty}=\\&\\&-\frac{2}{s}e^{-5s}+\frac 2se^0 +¿?=\\&\\&\text{como }s\ge 10\implies4-s\le 0\implies e^{(4-s)\infty}\to 0\\&\text{y además el denominador ayuda todavía mas a tender a 0}\\&\\&=\frac{-2e^{-5s}}{s}+ \frac 2s+0-\frac{e^{10(4-s)}}{4-s}=\\&\\&\frac{2-2e^{-5s}}{s}- \frac{e^{10(4-s)}}{4-s}\end{align}$$:
:
