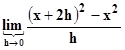Limites no encuentro la solución

Buenas noches tengo problemas con este ejercicio ya que no le entiendo muy bien.
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
1
Respuesta de Luis Alberto Candio Salcedo
1