Halla los puntos críticos, los intervalos en donde f es creciente o decreciente y construye la gráfica de

·

·

¡Hola Ana Belén!

Son varios ejercicios, ganaríamos todos si los mandas de uno en uno.

1)

Los puntos críticos son los que anulan la derivada.

f(x)=x^2-2x

f'(x) = 2x -2 = 0

2x = 2

x =1

Es un mínimo porque es una parábola con forma de U. Otra forma de verlo es con la derivada segunda

f''(x) = 2 >0 ==> mínimo

Y el punto crítico es (1, 1^2-2·1) = (1, 1-2) = (1,-1)

Y respecto al crecimiento o decrecimiento podemos aplicar de nuevo que es una parábola con forma de U, por lo que es decreciente hasta el mínimo y creciente después.

(-Infinito, 1) decreciente

(1, infinito) creciente.

Pero la forma general de hacerlo es con el signo de la derivada primera.

f'(x)=2x-2

Ya vimos que en x=1 valía 0. Tomamos un punto del intervalo anterior a x=1, por ejemplo 0

f'(0) = 2·0 - 2 = -2 < 0

Como la derivada es negativa, la función es decreciente en el intervalo

(-infinito, 1) decreciente

Y tomamos un punto del intervalo posterior, por ejemplo x=2

f'(2) = 2·2-2= 4-2 = 2 > 0

cono la derivada es positiva, la función es creciente en el intervalo

(1, + infinito) creciente

Algún dato más para la gráfica son los cortes con los ejes

x^2-2x=0

x(x-2) = 0

Y los cortes con el eje X sonson x=0, x=2

Y el corte con el eje Y es en y=0^2-2·0=0-0=0

Esta es la gráfica.

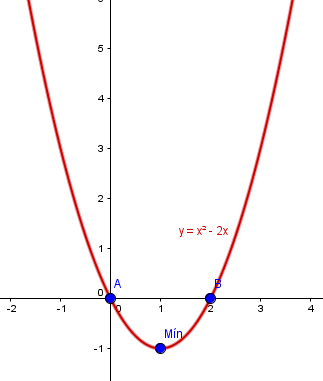
Y eso es todo, saludos.

:

: