¿Me Colaboran con el con el ejercicio 2 de 4. Calculo diferencial?
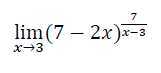
Espero me puedan colaborar. Los limites me tienden a enredar.
2 Respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
