Estudio del Departamento de Transporte
Un estudio del Departamento de Transporte de Illinois concluyó que 76.2% de quienes ocupaban los asientos delanteros de los vehículos utilizaba cinturón de seguridad. Esto significa que los dos ocupantes de la parte delantera utilizaban cinturones de seguridad. Suponga que decide comparar la información con el uso actual que se da al cinturón de seguridad, para lo cual selecciona una muestra de 12 vehículos. INFORME A PRESENTAR: Presente un informe en el que como mínimo incluya:
1.- ¿Esta situación cumple con los supuestos de la distribución binomial? Identifíquelos
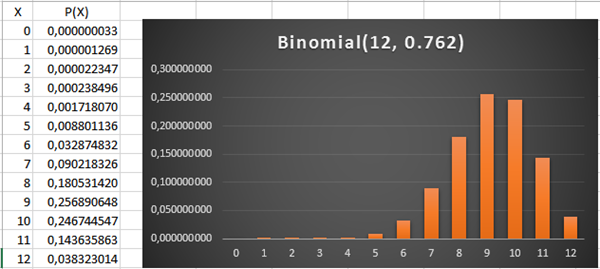
2.- Elabore un diagrama de barras para la distribución de probabilidad binomial que representa esta situación
3.- ¿Cuál es la probabilidad que los ocupantes de la parte delantera en exactamente 7 de los 12 vehículos seleccionados utilicen cinturones de seguridad?
4.- ¿Cuál es la probabilidad que los ocupantes de la parte delantera de por lo menos 7 de los 12 vehículos utilicen cinturón de seguridad?
5.- ¿Cuál es la probabilidad que los ocupantes de la parte delantera de máximo 7 de los 12 vehículos
6.- ¿Encuentre el valor esperado del número de vehículos en los que los ocupantes de la parte delantera utilizan el cinturón de seguridad?
1 Respuesta
'
'
¡Hola Juan Carlos!
1)
Una distribución binomial consiste en repetir una prueba n veces. La prueba solo puede presentar dos resultados éxito o fracaso con suma de esas dos probabilidades igual a 1. A la probabilidad de éxito se le llama p.
Y debe presentar la característica de que la probabilidad de cada prueba es independiente del resultado de las anteriores, es decir, que p es constante para todas las pruebas.
Esta situación no cumple por entero los requisitos de una distribución binomial, cuando salga un conductor con cinturon la probabilidad de que los otros lleven cinturón disminuirá algo y viceversa. Pero se supone que la cantidad de conductores es tan grande que esa diferencia es despreciable. Por tanto, podemos asumir que es una binomial casi perfecta. Es una B(12, 0.762)
n=12
p=0.762
·
2)
Y el diagrama de barras es este
·
3)
La fórmula de probabilidad de la binomial es:
$$\begin{align}&P(k) = \binom nk p^k(1-p)^{n-k}\\&\\&\text{Aplicamos la fórmula para x=7}\\&\\&P(x=7)=\binom{12}{7}0.762^7·0.238^{5}=0.09021832636\\&\\&4)\\&\\&\text{Ya tenemos la de 7, calculamos las de 8 hasta 12}\\&P(8) = \binom {12}{8} 0.762^{8}(1-0.762)^{12-8}=0.1805314199\\&\\&P(9) = \binom {12}{9} 0.762^{9}(0.238)^{3}=0.2568906479\\&\\&P(10)=\binom {12}{10} 0.762^{10}(0.238)^{2}=0.2467445467\\& \\&P(11)=\binom {12}{11} 0.762^{11}(0.238)=0.1436358629\\&\\&P(12)= 0.762^{12}=0.03832301385\\&\\&P(\ge7)=\sum_{k=7}^{12}P(k)=0.9563438176\\&\\&\\&5) \\&\\&P(<=7) = 1-P(>7)=1-[P(\ge7)-P(7)]=\\&\\&1-[0.9563438176-0.09021832636]=0.1338745087\end{align}$$Si no es así preguntame, si ya está bien valora la respuesta.
Saludos.
:
:
