Deducir que g(x) es menor o igual a 0?

Imagino que I quiere decir [1,e]

Las variaciones de g son

g(B)-g(A) = 1+ln(B) -B - (1+ln(A)-A)=A-ln(A)-B+ln(B)

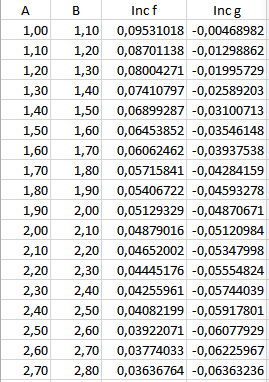
y la tabla es esta, incluyo también la de f de antes.

b)

Esto es lo que hice en el último ejercicio precisamente, para ello calculamos la derivada.

$$\begin{align}&g'(x)=\frac 1x-1=\frac{1-x}{x}\\&\\&\text{En el intervalo (1,e] se cumple}\\&\\&x\gt 0,\quad1-x\lt 0 \implies \frac{1-x}{x}\le0\\&\\&\text{Luego g es decreciente}\\&\\&\text{Y como }g(1)=1-ln\,1-1=1-0-1=0\\&\\&g(x)\lt 0 \;en \;(1, e]\\&\\&c)  f(x)=1 +ln(x)\\&\\&f(x)\lt x\iff\\&\\&1+ln(x)\lt x\iff\\&\\&1+ln(x)-x\lt 0\iff\\&\\&g(x)\lt 0\\&\\&\text{como demostramos arriba que }g(x)\lt 0\\&\text{volviendo el argumento hacia atras llegamos a}\\&f(x)\lt x \;en\; (1,e]\\&\end{align}$$

Y eso es todo, saludos.

:

: