Hallar las alturas del cono y cilindro para área superficie mínima

·

·

La función a optimizar es el área de la tolva. Llamaré x a la altura del cono y y a la del cilindro. El área lateral del cilindro es sencilla

Acil= 2pi·2y = 4pi·y

La del cono es más complicada

$$\begin{align}&A_{cono}=\pi rg= \pi·2·\sqrt{x^2+2^2}\\&\\&A(x,y)=2pi(2y+\sqrt{x^2+4})\\&\\&\text{Y el volumen de la tolva es}\\&\\&V(x,y)=\pi·2^2·y+\pi·2^2·\frac 13x\\&\\&V(x,y)=4pi\left(y+\frac x3 \right)\\&\\&\text{La ecuación de ligadura es}\\&\varphi(x,y) = 4pi\left(y+\frac x3 \right)-100=0\\&\\&\text{Y las ecuaciones de las derivadas parciales son}\\&\\&A_x+\lambda\varphi_x=0\\&A_y+\lambda\varphi_y=0\\&\\&2\pi \frac{x}{\sqrt{x^2+4}}+\lambda·\frac 43 \pi=0\\&\\&4\pi+\lambda ·4\pi = 0\implies \lambda = -1\\&\\&\frac{x}{\sqrt {x^2+4}}-\frac{2}{3}=0\\&\\&\frac{x}{\sqrt {x^2+4}}=\frac{2}{3}\\&\\&3x=2 \sqrt{x^2+4}\\&\\&9x^2=4x^2+16\\&\\&5x^2=16\\&\\&x^2=\frac {16}5\\&\\&x =\frac 4{\sqrt 5}= \frac{4 \sqrt 5}{5}\approx 1.788854382 pies\\&\\&y=\frac{100}{4\pi}- \frac x3 = \frac {25}{\pi}- \frac {4 \sqrt 5}{15}\approx 7.361462361pies\\&\\&\text{Comprobemos al menos que el volumen está bien}\\&\\&V=\pi·2^2· 7.361462361+\pi·2^2·\frac 131.788854382=100\end{align}$$

Y esta es la tabla Excel que muestra que muy bien puede ser esa la respuesta.

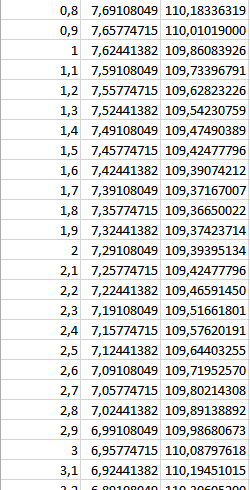
Y eso es todo, saludos.

:

: