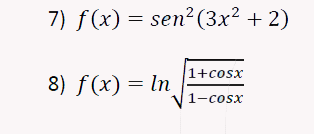---
---
¡H o la Lirio!
Pondré primero las reglas:
$$\begin{align}&(f+g)'=f'+g'\\&(kf(x))' = k·f'(x)\\&\left( \frac fg\right)'=\frac{f'g-fg'}{g^2}\\&(f[g(x)])'=f'([g[x)]·g'(x)\\&(x^n)' = nx^{n-1}\\&(sen\,x)'= \cos x\\&(ln\,x)=\frac 1x\\&\\&\\&7) f(x)=sen^2(3x^2+2)\\&\\&f'(x)= 2·sen^{2-1}(3x^2+2)·[sen(3x^2+2)]'=\\&\\&2sen(3x^2+2)·\cos(3x^2+2)·(3x^2+2)'=\\&\\&2 sen(3x^2+2)·\cos(3x^2+2)·6x=\\&\\&12x·sen(3x^2+2)·\cos(3x^2+2)=\\&\\&\text{haz esto solo si has dado trigonometría avanzada}\\&\\&=6x·sen(6x^2+4)\\&\\&---------------------\\&\\&8)f(x)=ln \sqrt{\frac{1+\cos x}{1-cosx}}\\&\\&\text{Si la quieres resolver así te puedes volver medio loco}\\&\text{Hay que simplificarla antes por propiedades de logaritmos}\\&\\&f(x)=\frac 12 ln\left(\frac{1+\cos x}{1-\cos x} \right)=\frac 12[ln(1+\cos x)-ln(1-cosx)]\\&\\&f'(x)= \frac 12\left(\frac{-sen\,x}{1+cosx}-\frac{senx}{1-cosx} \right)=\\&\\&\frac{1}{2}\left(\frac{-sen\,x+sen\,x·\cos x-sen\,x-sen\,x·\cos x}{1-\cos^2x} \right)=\\&\\&\frac 12·\frac{-2 sen\,x}{sen^2x}=-\frac{1}{sen x}=-csc\,x\\&\\&\end{align}$$Y ya está. S al u d o s.
"
"