Resolver los siguientes ejercicios de calculo 1
Sobre todo el primer ejercicio que es demostración.
2 respuestas
·
·
¡Hola Gino!
El primer ejercicio es verdadero. Se llama igualdad ciclotómica y la demostración es una simple comprobación.
$$\begin{align}&(x-y)(x^{n-1}+yx^{n-2}+...+xy^{n-2}+y^{n-1})=\\&\\&x^n+yx^{n-1}+..............+x^2y^{n-2}+xy^{n-1}+\\&\quad-yx^{n-1}-y^2x^{n-2}-..............-xy^{n-1}-y^n=\\&\\&x^n-y^n\end{align}$$Si quieres pruébalo con números n pequeños y verás como se cancelan entre sí todos los términos salvo x^n y -y^n
.
2)
$$\begin{align}&|x^2-3|+2\le |x^2-1|\\&\\&\text{Distinguimos estos casos}\\&\\&1) \quad x^2-1\le0\implies x^2\le 1\implies x\in[-1,1]\implies\\&x\in[-\sqrt 3,\sqrt 3]\implies x^2\le3\implies x^2-3\le0\\&\text{Luego la desigualdad es así}\\&3-x^2+2\le 1-x^2\\&5\le1\\&\text{no hay solución}\\&\\&\\&2)\quad x^2-1\ge0\; pero\; x^2-3\le0\\&3-x^2+2\le x^2-1\\&6\le 2x^2\\&3\le x^2\\&\text{O sea, debe ser}\\&3\le x^2\le 3\\&x=\pm \sqrt 3\\&\\&3)\quad x^2-3\gt0\implies x^2-1\gt0\\&\text{queda este desigualdad}\\&x^2-3+2\le x^2-1\\&-1\le-1\\&\text{se cumple siempre luego}\\&x^2\gt 3\\&\\&\text{Uniendo las soluciones 2 y 3 tenemos la total}\\&\\&x^2\ge 3\\&\\&\text{o puesto de otra forma}\\&\\&S=(-\infty,-\sqrt 3]\cup[\sqrt 3,\infty)\\&\\&\\&\end{align}$$He aquí la gráfica de
f(x) = |x^2-3|+2 - |x^2-1|
Será la solución de la desigualdad cuando f(x)<=0
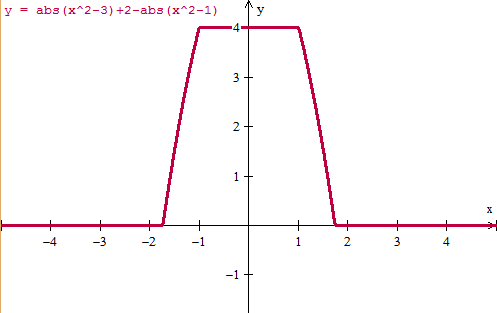
Lo cual verifica la respuesta dada.
Y no se pueden mandar tantos ejercicios, hay que mandarlos de uno en uno.
S a l u d o s.
:
:
Gino, son muchos ejercicios para una sola pregunta, por lo pronto te digo que el 1 no es cierto, para esto veamos que ocurre si n=2
$$\begin{align}&Izquierda:\\&x^2-y^2\\&Derecha:\\&(x-y)(x^{2-1}+x^{2-2}y+xy^{2-2}+y^{2-1})=(x-y)(x+y+x+y)=\\&(x-y)(2x+2y)=2x^2+2xy-2xy-2y^2=2x^2-2y^2\end{align}$$Así que no es cierto (salvo que haya alguna otra restricción que no aclaraste.
El ejercicio 2 veo de hacerlo en breve, porque no me está funcionando el editor de ecuaciones :(
A ver si puedo subir el ejercicio 2...
$$$$
Evidentemente tengo un problema con el editor, voy a intentar ponerlo acá pero no se si se va a entender :(,
considerá que la solución es x = [sqrt(3), + infinito)
|x^2-3|+2 <= |x^2-1|
Si x^2-3 >= 0 ENTONCES x >= sqrt{3}
El lado derecho también será positivo y puedo sacar todos los módulos
Si x >= sqrt{3}
x^2-3+2 <= x^2-1
x^2-1 <= x^2-1
0 <= 0 (Vale!)
Si x<sqrt{3}
Se dividen dos casos:
a) |x| < 1
b) |x| >= 1
Vamos por el caso a), para sacar los módulos, tenemos que cambiar los signos en ambos lados
-x^2+3+2 <= -x^2+1
5 <= 1 (NO vale para ningún x)
Para el caso b), para sacar los módulos, tenemos que cambiar los signos de la izquierda, pero en la derecha quedan como están
-x^2+3+2 <= x^2-1
-x^2+5 <= x^2-1
6 <= 2x^2 ENTONCES x >= sqrt{3} (Que ya lo teníamos)
Conclusión: x PERTENECE [sqrt{3},+\infty)