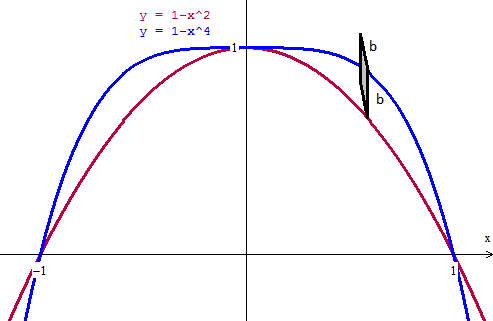
Volumen de un solido, base limitada por dos funciones.
Pues de nuevo con estos problemas... Me piden lo siguiente:
La base de un sólido es la región limitada por y=1-x^2 y y=1-y^4 . La sección transversal del sólido perpendicular al eje x es un cuadrado. Encuentre el volumen del sólido.
Al realizar el gráfico las dos parábolas son similares, mi idea era sumar los volúmenes, pero creo que no aplica... En resumen estoy perdidísima...
1 respuesta
·
·
¡Hola Angela!
Esto lleva un día colgado, ya había escrito bastante y no pudo mandarse. A ver si por lo menos en este rato que parece funciona te puedo mandar el dibujo.
Para ver la perspectiva bien tines que mirar de derecha a izquierda el cuadradito que mal he dibujado. Pues por todo el intervlo entre -1 y 1 hay cuadrados de esos de distinto tamaño y tienes que hacer la integral de las áreas de ellos. El lado del cuadrado será la diferencia entre las dos funciones.
$$\begin{align}&V=\int_{-1}^1 [(1-x^2)-(1-x^4)]^2dx=\\&\\&\int_{-1}^1(x^4-x^2)^2dx=\int_{.1}^1(x^8-2x^6+x^4)dx=\\&\\&\left[\frac {x^9}{9}-\frac{2x^7}{7}+\frac{x^5}{5} \right]_{-1}^1=\\&\\&\frac 19-\frac 27+\frac 15+\frac 19-\frac 27+\frac 15=\\&\\&\frac 29-\frac 47+\frac 25=\frac{70-180+126}{315}=\frac{16}{315}\end{align}$$Y eso es todo, ojalá se pueda mandar.
Sa lu dos.
:
:
¡Gracias! Si lo pude ver... y he entendido que no es una suma sino una resta y ahora todo tiene mucho más sentido!
De nuevo mil gracias por esta dispuesto a ayudarme constantemente!
