Como resolver ejercicio de parcial

·

¡Hola Matías!

También se puede resolver por variables separables

$$\begin{align}&\frac {dp}{dt}=0.4p-200\\&\\&\frac{dp}{0.4p-200}=dt\\&\\&\frac{ln(0.4p-200)}{0.4}=t+C\\&\\&ln(0.4p-200)=0.4t + C\\&\\&0.4p + 200 = Ce^{0.4t}\\&\\&p = Ce^{0.4t}-\frac{200}{0.4}\\&\\&p(t)=Ce^{0.4t}-500\\&\\&p(0)=20\implies C-500= 20\implies C=520\\&\\&p(t)=520e^{0.4t}-500\end{align}$$

Y eso es todo, sa lu dos.

:

:

¡Gracias! 

me acabo de dar cuenta que lineal no se podía o eso creo por que me dio un resultado diferente a mi en el examen por que p´- 0,4p igualado a -200  y valuar una lineal así esta mal por que -200 debería estar en función de t.

Si, si que es lineal y se puede calcular por el método de las lineales de coeficientes constantes, resolviendo primero la homogénea con la ecuación característica y luego una solución particular de la completa mediante variación de parámetros

$$\begin{align}&p' =0.4p -200\\&\\&p'-0.4p = -200\\&\\&k -0.4 = 0\\&\\&k=0.4\\&\\&p_{GH}= Ce^{0.4t}\\&\\&p_P = A\\&\\&p'_P=0\\&\\&0-0.4A=-200\\&\\&A = \frac{200}{0.4}=500\\&\\&p_P=400\\&\\&p(t) = Ce^{0.4t}+500\\&\\&\text{Y como }P(0)=20\\&\\&20 = C + 500\\&\\&C=-480\\&\\&p(t)=-480e^{0.4t}+500\end{align}$$

Como puedes ver da distinto de antes, es que antes cambié un signo sin ningun motivo, lo hago bien ahora.

$$\begin{align}&\frac {dp}{dt}=0.4p-200\\&\\&\frac{dp}{0.4p-200}=dt\\&\\&\frac{ln(0.4p-200)}{0.4}=t+C\\&\\&ln(0.4p-200)=0.4t + C\\&\\&0.4p - 200 = Ce^{0.4t}\\&\\&p = Ce^{0.4t}+\frac{200}{0.4}\\&\\&p(t)=Ce^{0.4t}+500\\&\\&p(0)=20\implies C+500= 20\implies C=-480\\&\\&p(t)=-480e^{0.4t}+500\end{align}$$

Claro está, la gráfica debe ser otra.

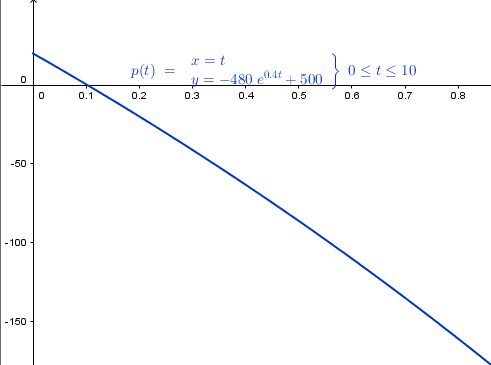
Y eso es tood, perdona por el fallo.

Sa lu dos.

:

: