Cómo se resuelve este ejercicio de área bajo la curva?
Instrucciones:
- Dibuja en un esquema la región encerrada por las curvas de las funciones dadas.
- Decide si integrar con respecto a x o y.
- Dibuja un rectángulo típico de aproximación, marca su altura y su ancho.
- Calcula el área de la región de las siguientes funciones:
y=x, y=3x, x+y=4
1 Respuesta
·
·
¡Hola Miguel Ángel!
Hacemos la gráfica. Vemos que tanto si integramos respecto de x como si lo hacemos respecto de y vamos a tener que dividir la región en dos trozos, luego no habiendo ninguna ventaja integramos respecto de x que es lo normal.
Los puntos de intersección de las rectas ya nos los da la gráfica pero vamos a calcularlos analíticamente para estar seguros del todo, y porque alguna vez calcularemos áreas sin hacer la gráfica y entonces si es necesario calcularlos con cuentas.
x=3x
x=0
·
y=3x
x+y=4
x+3x=4
4x=4
x=1
·
y=x
x+y=4
x+x=4
x=2
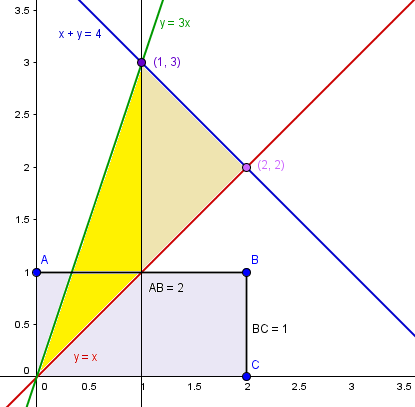
Y el área será
$$\begin{align}&A_1=\int_0^1(3x-x)dx=\int_0^12x\;dx=x^2\bigg|_0^1=1\\&\\&A_2=\int_1^2[(4-x)-x]dx=\int_1^2(4-2x)dx=\\&\\&\left[4x-x^2\right]_1^2= 8-4-4+1=1\\&\\&\text{Luego el área total es:}\\&\\&A=1+1=2\end{align}$$Y lo del rectángulo es un rectángulo que tiene como base el dominio de integración y la altura necesario para que el área sea la misma que la de la integral.
El dominio de integración es [0, 2], luego la base mide 2
Y el área debe ser 2, luego la altura será 2/2 = 1
Ahí lo tienes pintado.
Y eso es todo, sa lu dos.
:
:
