¿Cómo desarrollo funciones continuas y discontinuas y su gráfica?

·

·

¡Hola Elizabeth!

Los polinomios son por ejemplo funciones continuas, toda recta, parábola o polinomio de grado superior es un a función continua.

Ahora sobre la forma que tengas de graficarla yo no sé como os habrán enseñado, lo haré con una tabla de datos.

La función será:

f(x) = -x^2 + 2x + 10

Por ejemplo para x=-2, -1, 0, 1 y 2

f(-2) = -4 -4 + 10 = 2

f(-1) =-1-2 + 10 = 7

f(0) = 10

f(1) = -1+2+10 = 11

f(2) = -4+4+10 = 10

f(3) = -9+6+10 =7

f(4)=-16+8+10=2

Y si acaso puedes añadir si lo sabes que la coordenada x del vértice es

-b/2a = -2 / -2 = 1

Por lo que el vértice es (1,11)

También podrías añadir los cortes con el eje X, lo que pasa es que esta vez son feos.

$$\begin{align}&-x^2+2x+10=0\\&\\&x^2 - 2x -10=0\\&\\&x=\frac{2\pm \sqrt{4+40}}{2}= 1\pm \sqrt{11}\\&\\&x_1=-2.3166\\&\\&x_2=4.3166\end{align}$$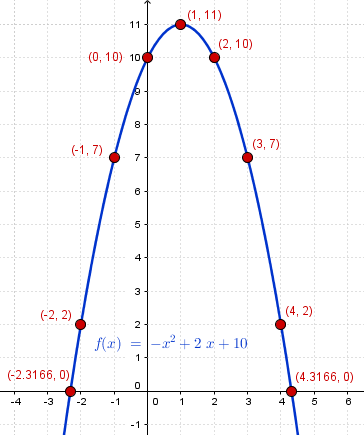

Es continua porque cumple la definición de función continua, esa de que el límite de la función en todo punto existe y coincide el valor de la función. Intuitivamente es continua porque se puede trazar sin levantar el lápiz del papel no hay saltos, o porque si aumentamos un poco el valor de la x, la y también crece solo un poco.

Y eso es todo, para la función discontinua mejor manda otra pregunta. Antes deberás valorar esta respuesta pinchando en el Excelente que verás abajo.

Saludos.

:

: