Completar con la ecuación de la elipse
Completar el siguiente cuadro con la fórmula de calculo vectorial de la elipse. Representación gráfica y ecuación.
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Edwin!
La ecuación canónica puede tener una de estas dos formas:
$$\begin{align}&\text{Si el eje de los focos es horizontal}\\&\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\\&\\&\text{Si el eje de los focos es vertical}\\&\frac{(x-h)^2}{b^2}+\frac{(y-k)^2}{a^2}=1\\&\\&(h,k) \text{ es el centro}\\&a \text{ es el semieje mayor}\\&b \text{ es el semieje menor}\\&\\&\text{Con esto tendremos:}\\&\\&1)\; Ecuación:\quad \frac{x^2}{25}+\frac{y^2}{16}=1\\&\\&2)\;Centro=(0,0),\quad a=6,\quad b=1\\&\\&3) \text{¡Ojo! Estamos en el segundo caso de ecuación}\\&\text{ya que el denominador de la y es el mayor}\\&\\&Centro=(2,0),\quad a=4,\quad b=3\end{align}$$Y las gráficas son estas:
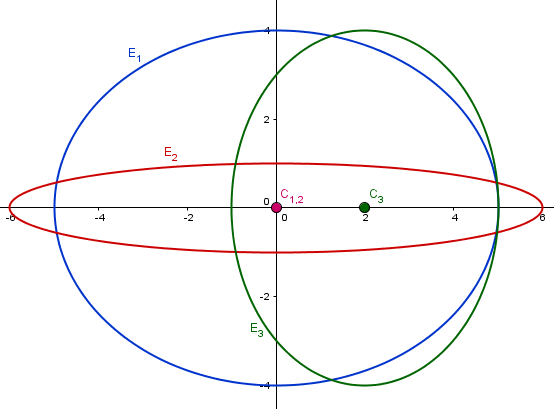
La azul es la primera, la roja la segunda y la verde la tercera.
Y eso es todo, saludos.
:
:
