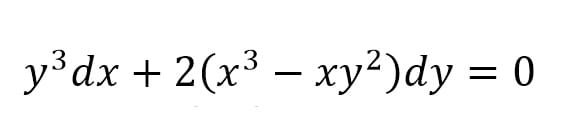Ejercicio de Ecuaciones diferenciales exactas

·

·

¡Hola JB Tech!

El 90% de las veces que me llega un anunciado diciendo que son ecuaciones diferenciales exactas no lo son, en su lugar son homogéneas, tal como pasa aquí.

No es exacta porque:

My= 3y^2

Nx = 6x^2 - 2y^2

Pero sí que es homogénea como decía:

$$\begin{align}&y^3dx + 2(x^3-xy^2)dy = 0\\&\\& 2(x^3-xy^2)dy=-y^3dx\\&\\&\frac {dy}{dx}=-\frac{y^3}{2(x^3-xy^2)}\\&\\&y=ux\\&\\&\frac {dy}{dx}=\frac{du}{dx}x+u=-\frac{u^3x^3}{2(x^3-x^3u^2)}\\&\\&\frac{du}{dx}x+u=-\frac{u^3}{2(1-u^2)}\\&\\&\frac{du}{dx}x=-\frac{u^3}{2(1-u^2)}-u=\frac{-u^3-2u+2u^3}{2(1-u^2)}\\&\\&\frac{du}{dx}x=\frac{u^3-2u}{2(1-u^2)}\\&\\&\frac{2(1-u^2)}{u^3-2u}du = \frac {dx}x\\&\\&2\int \frac{1-u^2}{u^3-2u}du = ln\,Cx\end{align}$$

Esa integral que queda te dejo que la hagas tú, o si no puedes me la mandas en otra pregunta.

Sa lu dos.

:

: