Como resuelvo estos problemas de limites
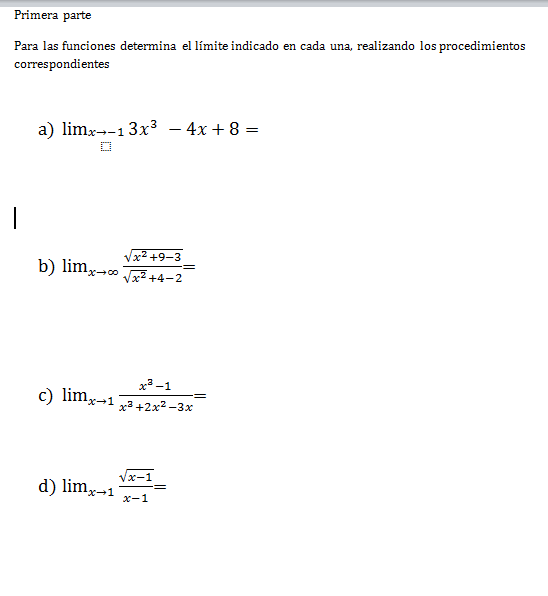

Por favor necesito ayuda ya que no me dan referencia sobre estos temas ni ejemplos y estoy desesperada
3 respuestas
Respuesta de Valero Angel Serrano Mercadal
1
Respuesta
1
Respuesta de Gustavo AR Imagen
1
