Como resolver ejercicios, limites de identidades trigonométricas
Busco un método falcil de entender para resolver estos ejercicios de matemáticas de indentidades trigonométricas
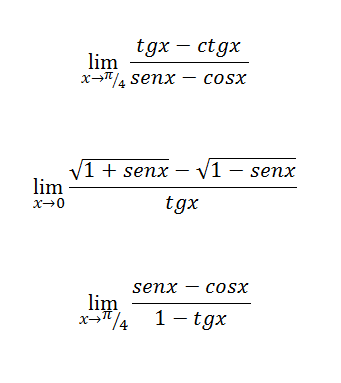
2 respuestas
;)
Hola Daniel!
Las indeterminaciones con expresiones radicales, se suelen resolver multiplicando y dividiendo por la expresión conjugada (la expresión conjugada de una resta de radicales es su suma)
$$\begin{align}&\lim_{x \to 0}\frac{ \sqrt{1+senx}- \sqrt {1-senx}}{tanx}=\frac{1-1}{0}=\frac{0}{0}=\\&\\&\lim_{x \to 0}\frac{ \sqrt{1+senx}- \sqrt {1-senx}}{tanx}·\frac{ \sqrt{1+senx}+\sqrt {1-senx}}{\sqrt{1+senx}+\sqrt {1-senx}}=\\&\\&(A+B)(A-B)=A^2-B^2\\&\\&=\lim_{x \to 0}\frac{ (\sqrt{1+senx})^2- (\sqrt {1-senx})^2}{tanx (\sqrt{1+senx}+\sqrt {1-senx})}=\\&\\&\\&\lim_{x \to 0}\frac{1+senx-(1-senx)}{tanx(\sqrt{1+senx}+\sqrt {1-senx})}=\\&\\&\lim_{x \to 0}\frac{2senx}{\frac{senx}{cosx}(\sqrt{1+senx}+\sqrt {1-senx})}=\\&\\&\lim_{x \to 0}\frac{2cosx}{(\sqrt{1+senx}+\sqrt {1-senx})}=\frac{2·1}{1+1}=1\\&\\&\\&\\&\\&\\&\end{align}$$saludos
Y recuerda votar
;)
;)
·
·
¡Hola Daniel!
Haré el primero que veo que no está hecho.
$$\begin{align}&\lim_{x\to \pi/4} \frac{tgx-ctgx}{senx-cosx}= \frac{\frac{\sqrt 2}{2}-\frac{\sqrt 2}{2}}{\frac{\sqrt 2}{2}-\frac{\sqrt 2}{2}}=\frac 00\\&\\&\text{Lo ponemos todo en función el seno u el coseno}\\&\\&\lim_{x\to \pi/4} \frac{\frac{sen\,x}{\cos x}-\frac{\cos x}{senx}}{senx-cosx}=\\&\\&\lim_{x\to \pi/4} \frac{\frac{sen^2x-\cos^2x}{senx·\cos x}}{senx -cosx} =\\&\\&\lim_{x\to \pi/4} \frac{sen^2x-\cos^2x}{senx·cosx(senx-cosx)}=\\&\\&\lim_{x\to \pi/4} \frac{(senx+cosx)(senx-cosx)}{senx·cosx(senx-cosx)}=\\&\\&\lim_{x\to \pi/4} \frac{senx+cosx}{senx·cosx}= \frac{\frac{\sqrt 2}{2}+\frac {\sqrt 2}{2}}{\frac{\sqrt 2}{2}·\frac{\sqrt 2}{2}}=\frac{\sqrt 2}{\frac 24}=2 \sqrt 2\end{align}$$Y eso es todo, como ya ves hacemos un ejercicio por pregunta, si quieres el tercero manda una pregunta nueva con él después de haber valorado con excelente las dos respuestas que te hemos dado.
Saludos.
:
:
Veo que has votado normal y aparte no veo que hayas votado a Lucas. No te cuesta nada votar Excelente, puedes hacerlo abajo pinchando donde pone Votada y hay que votar a todos los expertos que respondieron bien. Es así como conseguirás que otra vez queramos responder tus preguntas, pues si no votas adecuadamente no querremos.
Saludos.
:
: