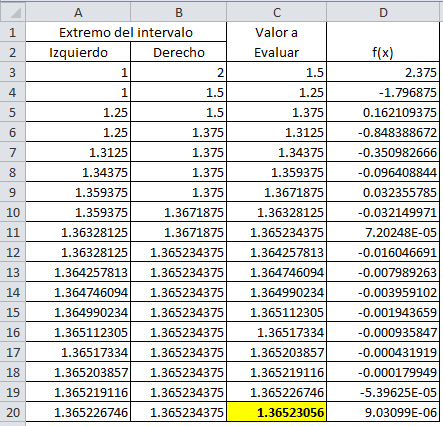
Demostrar que f(x) = x3 + 4x2 – 10 tiene una raíz en [1, 2] y utilizando el Método de bisección determine una aproximación a
Agradezco su respuesta en este ejercicio de métodos numéricos
2 respuestas
Para demostrar que tiene una raíz, evaluamos la función en los extremos del intervalo dado
f(1) = 1^3 + 4*1^2 - 10 = -5 (<0)
f(2) = 2^3 + 4*2^2 - 10 = 14 (>0)
Como la función es continua y cambia de signo en el intervalo, entonces podemos asegurar que tiene una raíz
Para el método de bisección te dejo una imagen, ya que lo voy a hacer en Excel
Por si te interesa, te dejo las fórmulas de la fila 4 (que deberías copiar hacia abajo)
[A4]: =SI(D3>0;A3;C3)
[B4]: =SI(D3>0;C3;B3)
[C4]: =(A4+B4)/2 .................(en [C3] va la misma fórmula)
[D4]: =C4^3+4*C4^2-10........(evaluación del polinomio, mismo que en [D3]
Por la precisión que te pidieron en la solución, la respuesta es 1.36523056
Salu2
Hola, no entiendo ese ejercicio. Eso queda así?
Si, la demostración que tiene una raíz es la primer parte
Y después lo que tenés que hacer es ir evaluando la función en la mitad del intervalo, si el resultado es < 10^(-5) estonces podés asumir que hallaste la raíz (puse ese número porque es el que te dan de tolerancia), si es negativo definís una mitad del intervalo y si es positivo definís la otra
Haciendolo en forma de algoritmo tenemos
Paso 1) a = 1 (extremo izquierdo)
Paso 2) b = 2 (extremo derecho)
{Ya sabemos que f(a) < 0 y que f(b) > 0}
Paso 3) c = (a + b) / 2
Paso 4) Si f(c) < 10^(-5) PARAR, la respuesta es c
Paso 5) Si f(c) < 0 hacer a = c, ir al paso 3
Paso 6) Si f(c) > 0 hacer b = c, ir al paso 3
Y eso es todo
Salu2
·
·
¡Hola Luk!
Hace un momento acabo de responder esa pregunta aquí: Método de bisección
Como verás tiene apariencia distinta y es un poco más general ya que el cálculo de extremos te sirve tanto para funciones crecientes como decrecientes. También se han hecho menos iteraciones porque en la que daba 0.720248E-5 < 0.001 ya teníamos la solución.
Es lo malo de este método, se puede tener una aproximación muy buena en un paso y luego vienen varios con aproximación peor.
Y eso es todo, no olvides valorar la respuesta.
Saludos.
:
: