Lee el siguiente planteamiento y responde utilizando alguno de los tres modelos matemáticos revisados (lineales, exponenciales
Lee el siguiente planteamiento y responde utilizando alguno de los tres modelos matemáticos revisados (lineales, exponenciales o logarítmicas).
Supongamos que tenemos un conejo macho y una hembra, y ellos producen cuatro conejitos (supón que dos son machos y dos hembras) que a su vez producen ocho. Y así, con la misma tasa de aumento, la próxima generación producirá 16, la próxima 32, la próxima 64 y así sucesivamente. Claro, estamos suponiendo en este modelo simple que el alimento es infinito y ¡Los conejos están muy libres! En ese caso, la función exponencial es
y = 2 x
O si designamos a C como el número de conejos y a t, como el número de periodos de reproducción de los conejos, se expresaría:
C = 2t
La base es ahora 2. Nota que si t = 1, C = 2 lo que quiere decir que en el momento inicial (en este modelo consideramos el inicio en t=1) se empieza con dos conejos.
Para esta función de los conejos C = 2t tabula los valores t desde cero hasta 15 de uno en uno, e identifica los números mencionados en el ejemplo del inicio de este ejercicio. Localiza los puntos en una gráfica, o utiliza un software graficador, para ver cómo es la gráfica. Puedes apoyarte del software Geogebra (http://www.geogebra.org/)
2. Menciona qué modelo matemático utilizaste y por qué es el modelo adecuado; además explica ¿de qué forma este modelo matemático te puede ayudar a comprender procesos de variación poblacional?
·
·
¡Hola Mindy!
Ya hace bastante tiempo contesté esta pregunta: Población de conejos
No olvides volver aquí para valorar la respuesta.
Ya está añadida la tabla y gráfica para 15 generaciones ya que han cambiado el enunciado, está al final de la pregunta.
1 respuesta más de otro experto
;)
Hola Mindy!
Eso es un modelo exponencial:
$$\begin{align}&y=2^x\end{align}$$
2. Cuando una población aumenta un mismo tanto por cien cada periodo 8(dias, años,...),
El modelo es del tipo. Piensa que en el ejemplo anterior, cuando decimos que cada generación se producen el doble de la anterior, podríamos haber dicho que cada generación aumenta el 100%.
Si una cantidad q, la multiplicamos por 2 equivale a un aumento del 100%:
$$\begin{align}&q+\frac{100}{100}q=q+q=2q\end{align}$$Si por ejemplo la población de un país aumenta un 10% cada año:
$$\begin{align}&P_0+\frac{10}{100}P_0=1.10 P_0\end{align}$$equivale a multiplicarla cada año que pasa por 1.10.
Luego el segundo año:
$$\begin{align}&P=P_0(1.10)(1.10)\\&P=P_0(1.10)^2\\&año\ 3:\\&P=P_0(1.10)^3\\&\\&P(t)=P_0(1.10)^t\end{align}$$Donde P_0 es la población del año 0 (de referencia)
T es el tiempo en años transcurridos.
Si la población aumenta un r% cada año. Tendremos:
$$\begin{align}&P(t)=P_0(1+r)^t\end{align}$$es el modelo exponencial que explica estos procesos de variación poblacional.
Saludos
;)
;)
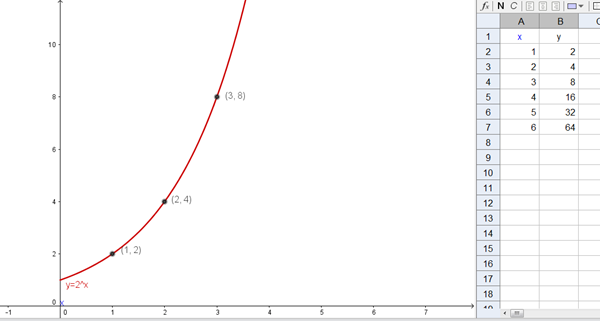
Maestro Valero efectivamente usted respondió a este problema hace tiempo, pero ahora le hicieron un pequeño cambio aquí (Para esta función de los conejos C = 2t tabula los valores t desde cero hasta 15 de uno en uno) el que usted resolvió era hasta 10 y este es hasta 15 además nos podría incluir por favor la gráfica en geogebra. gracias - Anonma Rosas H
Ya está la tabla, gráfica y fichero para 15 generaciones, Anonma. - Valero Angel Serrano Mercadal