Hallar la derivada para los siguientes ejercicios
Como encontrar la derivada para las siguientes funciones...
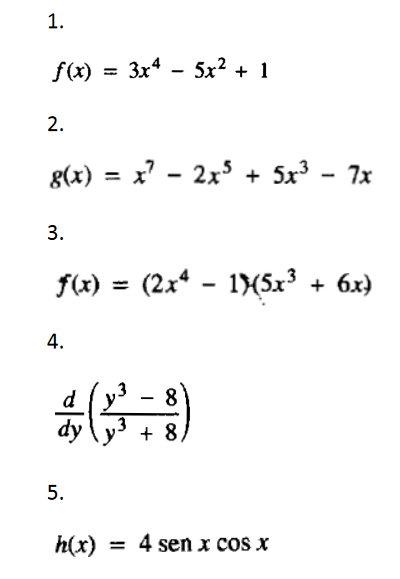
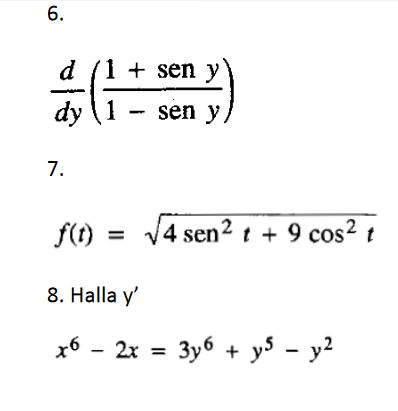
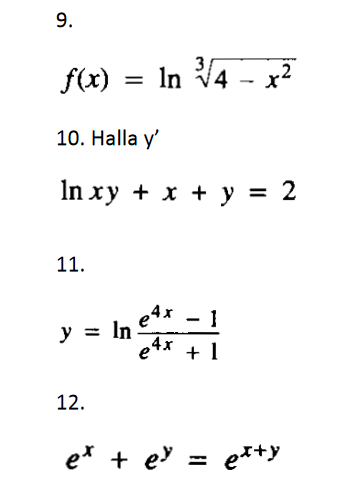
Respuesta de Valero Angel Serrano Mercadal
2
2 respuestas más de otros expertos
Respuesta
2
Respuesta de Lucas m
2

