Resolver los siguientes ejercicios calculo
Realizar lo solicitado en las imágenes...

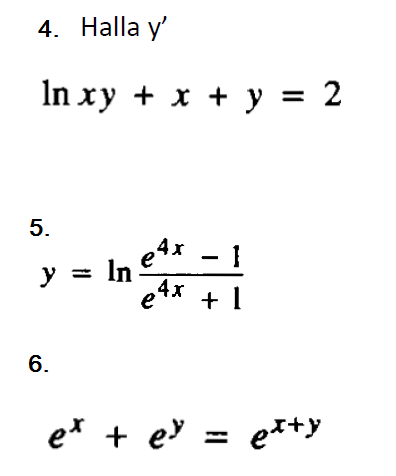
Respuesta de Valero Angel Serrano Mercadal
1
1 respuesta más de otro experto
Respuesta
1
