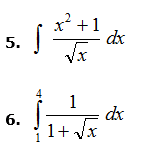Como resuelvo Integral Indefinida - Integral Definida de los siguientes ejercicios?
Aplicando las propiedades y definición de integral, resolver las siguientes integrales mostrar paso a paso
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
3
·
·
¡Hola Lirio!
La primera es muy sencilla:
$$\begin{align}&\int \frac{x^2+1}{\sqrt x}dx = \int \left(x^{\frac 32}+x^{-\frac 12}\right)dx=\\&\\&\frac{x^{\frac 52}}{\frac 52}+ \frac{x^{\frac 12}}{\frac 12}+C = \frac 25 \sqrt{x^5}+2 \sqrt x+C\\&\\&----------------\\&\\&\int_1^4 \frac{1}{1+\sqrt x}dx=\\&\\&\text{hacemos un cambio de variable y límites de integración}\\&\\&t=1+\sqrt x \implies \sqrt x=t-1\\&dt= \frac{dx}{2 \sqrt x}= \frac {dx}{2(t-1)}\implies dx= 2(t-1)dt\\&x=1\implies t=1+ \sqrt 1 = 2\\&x=4\implies t=1 + \sqrt 4=3\\&\\&=\int_2^3 \frac{1}{t}·2(t-1)dt = \int_2^3\left(2- \frac 2t\right)dt=\\&\\&\left[ 2t - 2 \,ln\,t \right]_2^3=6-2ln3-4+ 2ln2 = 2+ln4-ln9\\&\end{align}$$Y eso es todo, saludos.
:
:
