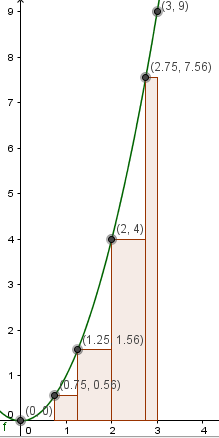
Como puedo resolver la funcion f(x)= x2, 0 ≤ x ≤ 3, para Δ: x0 = 0, x1 = 3/4, x2 = 1 ¼, x3 = 2, x4 = 2 3/4, x5 = 3. Paso a pas
$$\begin{align}&f(x)= x2, 0 ≤ x ≤ 3, para Δ: x0 = 0, x1 = 3/4, x2 = 1 ¼, x3 = 2,\\&x4 = 2 3/4, x5 = 3.\\&\end{align}$$como la puedo resolver paso por paso
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
¡Gracias! Angel
Esto es lo que me pidieron en cada uno de los ejemplos que me dieron y una disculpa por no especificar lo que me pidieron :)
Encontrar la suma de Riemann para la función f(x) en el intervalo, indicado.
Hacer una gráfica de la función en el intervalo dado y mostrar los rectángulos cuyas medidas de área son los términos de la suma de Riemann, utilice tablas como en la guía para manejar los datos.
Si no te especifican más puedes elegir que el primer sumando tenga f(x0) o f(x1), yo lo haré con f(x0)
$$\begin{align}&S=\sum_{i=0}^{n-1}f(x_i)(x_{i+1}-x_i)\\&\\&S= 0^2\left(\frac 34 -0 \right)+\left(\frac 34\right)^2\left(\frac 54-\frac 34 \right)+\left(\frac 54\right)^2\left(2-\frac 54 \right)+2^2\left(\frac {11}4-2 \right)+\left(\frac {11}4\right)^2\left(3-\frac {11}4\right)=\\&\\&0+\frac{9}{16}·\frac 12+\frac{25}{16}·\frac 34+4·\frac 34+ \frac {121}{16}·\frac 14=\\&\\&\frac{9}{32}+\frac{75}{64}+3+\frac {121}{64}=\frac{18+75+192+121}{64}=\frac{406}{64}=\frac {203}{32}\end{align}$$Y esta es ka gráfica:
Y eso es todo, s a l u d o s.
::
;
