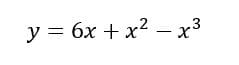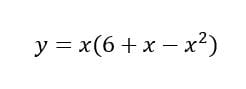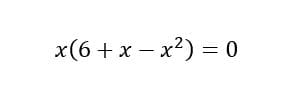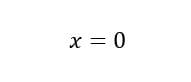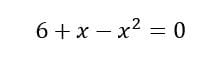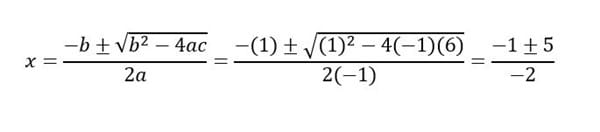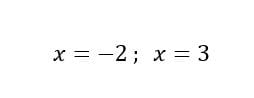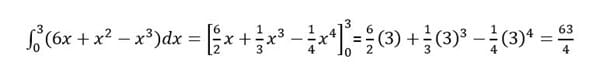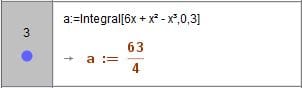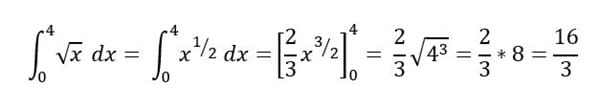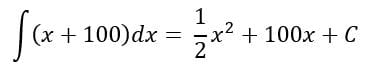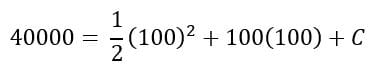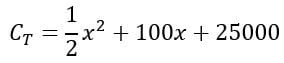Quien entiende sobre calculo integral
Cada ejercicio se debe resolver paso por paso, sin omitir ninguno, cuando se utilice una propiedad, definición o ley por favor enunciarla, así se fortalece el procedimiento utilizado. grafica del ejercicio 1 y 8
Con respecto al primer problema.
Primero debes encontrar las raíces de la ecuación.
Siendo la función.
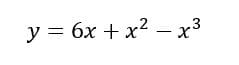
Primero despejemos la x del primer temino.
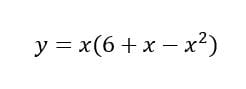
Con esto para encontrar las raíces, o lo que es lo mismo, la intersección de la gráfica con el eje "x" igualamos la ecuación a cero.
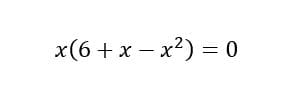
Con esto ya puedes ver parte de las intersecciones.
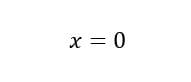
Esa es la primera raiz, la segunda seria con una ecuacion asi.
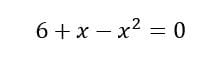
Para ello usamos la formula para resolver ecuaciones cuadraticas.
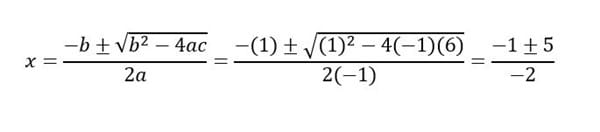
Resolviendo te quedan las sigueintes intersecciones.
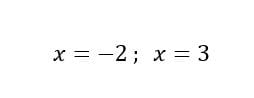
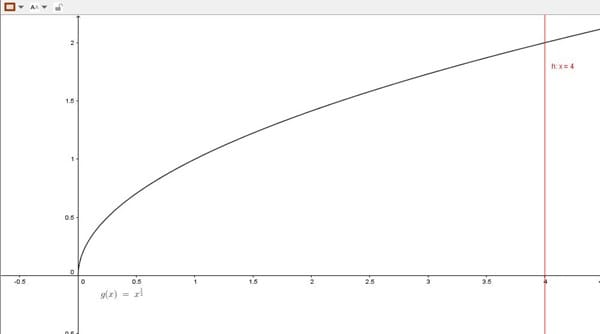
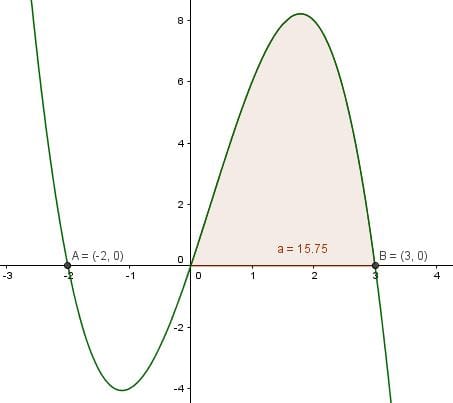
Ahora debes realizar la integral, antes de eso te mostrare como es la gráfica de la función.
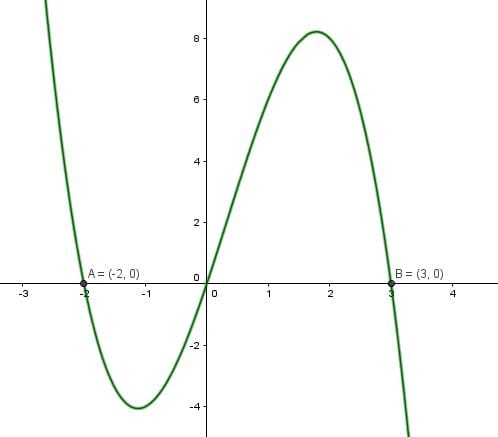
La funcion quedaria defina de esta manera.
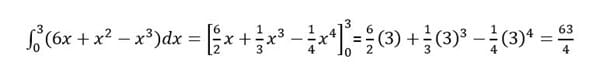
Como puedes ver la integral se realiza entre el 0 y el 3, también puedes ver el procedimiento.
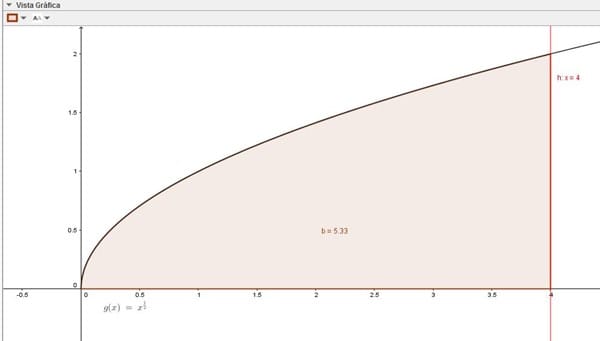
También te dejo, la gráfica ashurada de la integral y el resultado utilizando el programa GeoGebra.
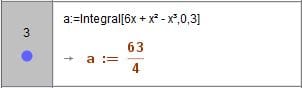
Espero te sirva. Si deseas deseas que resuelva la siguiente me comentas, que estés bien.
¡Gracias! por fa colaborame con los otros do
Te resolveré la segunda (8), intenta resolver sola la ultima, no esta tan complicada. Con respecto al problema en si.
El área se determina entre el eje "x", la función y la recta x=4, esta recta es vertical. La gráfica queda como ves en la imagen.
Como se aprecia, debes integrar desde los limites, cero y cuatro. La integral queda de esta manera.
Esto se puede constatar en el programa GeoGebra.
Eso es todo, espero haber sido claro en la explicación. Intenta hacer el ultimo.
Slds que estes bien. Ronald
¡Gracias! Estoy errada en el ultimo no me da me colabora please
Por nada. Solo que no logro leer bien el enunciado.
La función que describe el costo marginal de fabricar un producto es C'(x)=x+100 donde x es el numero de unidades producidas se sabe también que el costo total es $40000 cuando x=100 determine la función de costo total
¿No lo intentaras?
si lo intente pero no me da
Del ultimo problema recuerdo que la función marginal es la derivada de la función costo total.
Así pues lo que debes hacer es una integral de la función dada.
Con esto evaluas los valores que te dan, para determinar el valor de "C".
Despejas la variable y determinas que su valor es 25000.
Con esto tienes la función final.
Espero no estar errado. Si así fuera imagino que alguien más lo corregirá.
Slds Ronald.
