Resolver ecuación con por en el exponente y base distinta
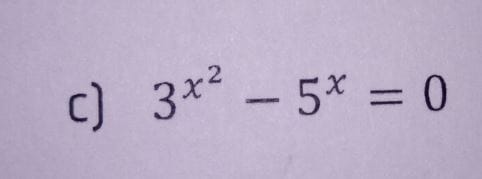
Buenos días:
¿Estoy intentando resolver esta ecuación aplicando logaritmos pero no consigo despejar la x. Alguien me puede echar una mano?
Respuesta de Kvothe Orwell
1

