Quien puede demostrar que S genera a R2
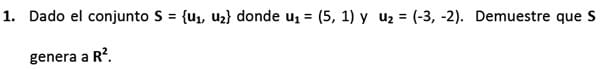
Amigos de todoexpertos les pido su colaboración en la solución de este ejercicio de álgebra lineal.
Respuesta de Lucas m
1
1 respuesta más de otro experto
Respuesta de Kvothe Orwell
1

