Analisis Matematico I Funcion Continua ¿? Demostrar
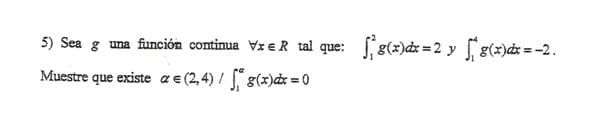
Hola expertos, ¿me ayudan con este ejercicio?
1 respuesta
Respuesta de Lucas m
2
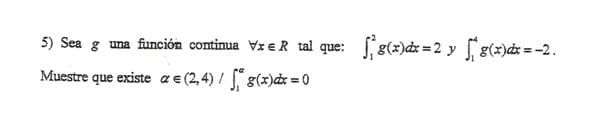
Hola expertos, ¿me ayudan con este ejercicio?
